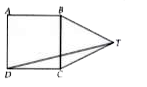
In the given diagram, ABCD is a square and Δ BCT is an equilateral triangle. ∠ BTD equals
30∘
15∘
45∘
35∘
The correct Answer is:C
Step by step video, text & image solution for In the given diagram, ABCD is a square and Delta BCT is an equilateral triangle. angle BTD equals by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- POLYGONS AND QUADRILATERALS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALS EXERCISE - SELF ASSESSMENT SHEET - 23
10 Videos
- POLYGONS AND QUADRILATERALS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALS EXERCISE - SELF ASSESSMENT SHEET - 23
10 Videos
- PERCENTAGE AND ITS APPLICATIONSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERCENTAGE AND ITS APPLICATIONSEXERCISE - SELFT ASSESMENT SHEET (SECTION-C DISCOUNT )
10 Videos
- PROBABILITYBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - SELF ASSESSMENT SHEET -29
10 Videos
Similar Questions
Knowledge Check
In the given figure,ΔCDE is an equlatel triangle triangle formed on a side CD of a square ABCD.Show that ΔADE≅ΔBCE.
 ARHSBSSSCAASDSAS
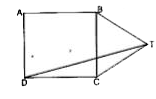
ARHSBSSSCAASDSASABCD is a square and ABE is an equilateral triangle outside the square then
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of theseABCD is a square and AOB is an equilateral triangle. What is the value of ∠DOC?
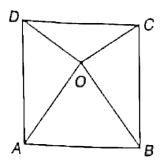 A120∘B150∘C125∘Dcan't be determined
A120∘B150∘C125∘Dcan't be determined
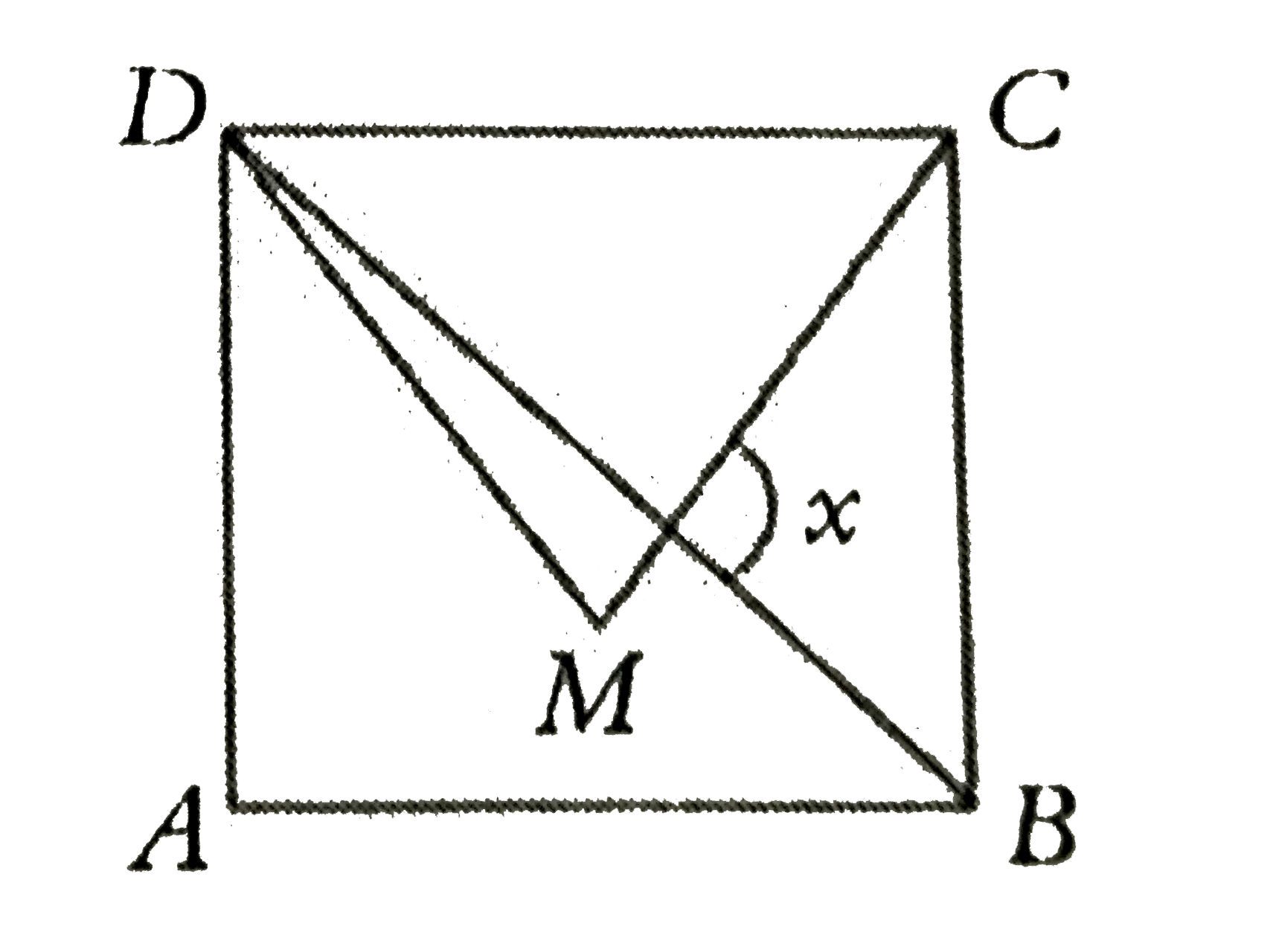
In the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.
View SolutionFind the perimeter of the given figure : BCDE is a square and ABC is an equilateral triangle.

View SolutionIn the given figure ABCD is a square with side 15 and BCE is an equilateral triangle. The ratio of the shaded region to the unshaded region is :
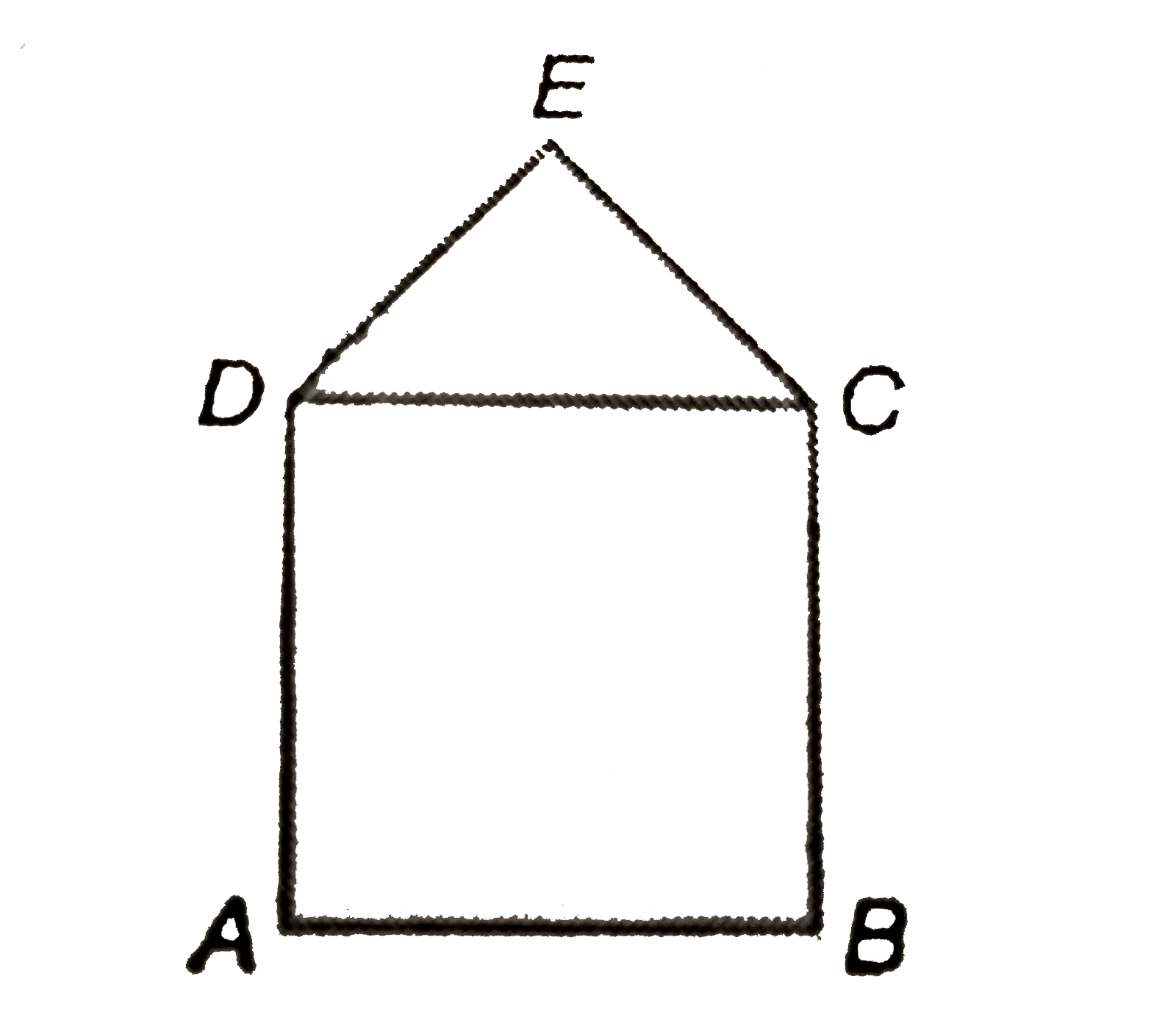
View SolutionIn the given figure, ABCD is a square of side 6 cm and CDE is an equilateral triangle. Find the perimeter of the figure.
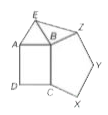
View SolutionIn the given figure , ABCD is a square BCXYZ is a regular pentagon and ABE is an equilateral triangle . What is the value (in degrees) of ∠EBZ ?
View Solution