ABCD is a rectangle with ∠BAC=48∘. Then ∠DBC equals
38∘
48∘
132∘
42∘
The correct Answer is:D
To solve the problem, we need to find the measure of angle DBC in rectangle ABCD, given that angle BAC is 48 degrees.
1. Understanding the Rectangle:
In rectangle ABCD, the diagonals AC and BD intersect at point O. Since ABCD is a rectangle, we know that opposite angles are equal, and adjacent angles are supplementary (sum to 90 degrees).
2. Identifying Angles:
We are given that angle BAC = 48 degrees. This angle is formed by diagonal AC and side AB.
3. Using Properties of Diagonals:
In a rectangle, the diagonals bisect each other. Therefore, angle AOB (where O is the intersection of diagonals) will also be equal to angle COD, and angle AOD will equal angle BOC.
4. Finding Angle DBC:
To find angle DBC, we can use the relationship between the angles in triangle BOC.
- Angle DBC is equal to angle CBA minus angle DBA.
- Since ABCD is a rectangle, angle CBA = 90 degrees (as it is one of the angles of the rectangle).
5. Calculating Angle DBA:
Since angle BAC = 48 degrees, angle DBA (which is the angle opposite to angle BAC in triangle AOB) will also be equal to angle BAC because the diagonals bisect each other. Therefore, angle DBA = 48 degrees.
6. Final Calculation:
Now we can calculate angle DBC:
Angle DBC=Angle CBA−Angle DBA=90∘−48∘=42∘
Conclusion:
Thus, angle DBC equals 42 degrees.
In rectangle ABCD, the diagonals AC and BD intersect at point O. Since ABCD is a rectangle, we know that opposite angles are equal, and adjacent angles are supplementary (sum to 90 degrees).
We are given that angle BAC = 48 degrees. This angle is formed by diagonal AC and side AB.
In a rectangle, the diagonals bisect each other. Therefore, angle AOB (where O is the intersection of diagonals) will also be equal to angle COD, and angle AOD will equal angle BOC.
To find angle DBC, we can use the relationship between the angles in triangle BOC.
- Angle DBC is equal to angle CBA minus angle DBA.
- Since ABCD is a rectangle, angle CBA = 90 degrees (as it is one of the angles of the rectangle).
Since angle BAC = 48 degrees, angle DBA (which is the angle opposite to angle BAC in triangle AOB) will also be equal to angle BAC because the diagonals bisect each other. Therefore, angle DBA = 48 degrees.
Now we can calculate angle DBC:
Angle DBC=Angle CBA−Angle DBA=90∘−48∘=42∘
Thus, angle DBC equals 42 degrees.
Topper's Solved these Questions
- POLYGONS AND QUADRILATERALS Book:S CHAND IIT JEE FOUNDATIONChapter:POLYGONS AND QUADRILATERALS Exercise:SELF ASSESSMENT SHEET - 23
Explore 10 Videos
- POLYGONS AND QUADRILATERALS Book:S CHAND IIT JEE FOUNDATIONChapter:POLYGONS AND QUADRILATERALS Exercise:SELF ASSESSMENT SHEET - 23
Explore 10 Videos
- PERCENTAGE AND ITS APPLICATIONSBook:S CHAND IIT JEE FOUNDATIONChapter:PERCENTAGE AND ITS APPLICATIONSExercise:SELFT ASSESMENT SHEET (SECTION-C DISCOUNT )
Explore 10 Videos
- PROBABILITYBook:S CHAND IIT JEE FOUNDATIONChapter:PROBABILITYExercise:SELF ASSESSMENT SHEET -29
Explore 10 Videos
Similar Questions
ABCD is a rectangle with ∠BAC=320. Determine ∠DBC.
View SolutionIn a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=40∘., then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है और CD एक ऐसी जीवा है कि ABCD समलम्ब है | यदि ∠BAC=40∘ है, तो ∠CAD ज्ञात करें|
View Solution
Knowledge Check
In the given figure, ABCD is a parallelogram, AD = AE, BAE is a straight line, ∠ABC=88∘,∠EAF=162∘and∠AFC=48∘. Then ∠ BCF equals.
 A18∘B28∘C22∘D32∘
A18∘B28∘C22∘D32∘In the given figure, RST is the tangent to the circle with centre O, at S. AOS is a straight line BO||RT and ∠ORS=46∘. Then ∠ BAC equals
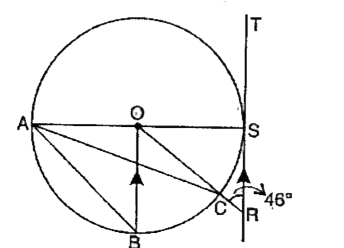 A22∘B46∘C23∘D32∘
A22∘B46∘C23∘D32∘ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and angle ADC = 140∘, ∠BAC is equal to:
ABCD एक चक्रीय चतुर्भज है जो इस प्रकार है कि AB इसे घेरने वाले वृत्त का व्यास है तथा कोण ADC = 140∘, है | कोण ∠BAC किसके बराबर है?A38∘B40∘C50∘D60∘
In a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=24∘ , then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है तथा CD एक ऐसी जीवा है कि ABCD एक समलम्ब बन जाता है | यदि ∠BAC=24∘ है, तो ∠CAD का मान ज्ञात करें |
View SolutionABCD is a rectangle with ∠ABD=400. Determine ∠DBC
View SolutionIn a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=25∘ , then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है तथा CD एक ऐसी जीवा है कि ABCD एक समलम्ब बन जाता है | यदि ∠BAC=25∘ है, तो ∠CAD का मान ज्ञात करें |
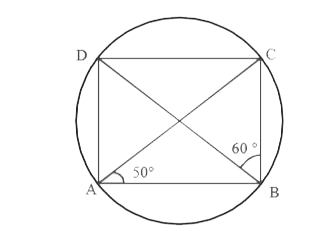
View SolutionIn fig., ABCD is a cyclic quadrilatreral. If ∠BAC=50∘ and ∠DBC=60∘, then find ∠BCD.
View SolutionIn a rectangle ABCD, AB= 15 cm ∠BAC=60∘ then BC is equal to
View Solution