ABCD is a rhombus. ∠DAB=2x+15∘,angle DCB =3x−30∘, angle BDC equals
To solve the problem, we need to find the angle BDC in the rhombus ABCD, given the angles DAB and DCB. Here’s a step-by-step solution:
Step 1: Set Up the Equations
We know that:
- Angle DAB = 2x + 15°
- Angle DCB = 3x - 30°
In a rhombus, opposite angles are equal. Therefore, we can set the two angles equal to each other:
2x+15°=3x−30°
Step 2: Solve for x
Now, we will solve the equation for x:
1. Rearranging the equation gives:
2x+15°+30°=3x
2x+45°=3x
2. Subtracting 2x from both sides:
45°=3x−2x
45°=x
Step 3: Find Angle DCB
Now that we have the value of x, we can find angle DCB:
Angle DCB=3x−30°
Substituting x = 45°:
Angle DCB=3(45°)−30°
Angle DCB=135°−30°
Angle DCB=105°
Step 4: Use Triangle Properties
Now, we will use the triangle properties in triangle DCB to find angle BDC. We know:
Angle DCB+Angle CBD+Angle BDC=180°
Let angle CBD = z and angle BDC = y. Since DC = BC in a rhombus, angles CBD and BDC are equal:
105°+z+y=180°
Since z = y:
105°+2y=180°
Step 5: Solve for Angle BDC
Now, we can solve for y:
1. Rearranging gives:
2y=180°−105°
2y=75°
2. Dividing by 2:
y=37.5°
Final Answer
Thus, the angle BDC is:
Angle BDC=37.5°
---
We know that:
- Angle DAB = 2x + 15°
- Angle DCB = 3x - 30°
2x+15°=3x−30°
Now, we will solve the equation for x:
1. Rearranging the equation gives:
2x+15°+30°=3x
2x+45°=3x
2. Subtracting 2x from both sides:
45°=3x−2x
45°=x
Now that we have the value of x, we can find angle DCB:
Angle DCB=3x−30°
Substituting x = 45°:
Angle DCB=3(45°)−30°
Angle DCB=135°−30°
Angle DCB=105°
Now, we will use the triangle properties in triangle DCB to find angle BDC. We know:
Angle DCB+Angle CBD+Angle BDC=180°
Let angle CBD = z and angle BDC = y. Since DC = BC in a rhombus, angles CBD and BDC are equal:
105°+z+y=180°
Since z = y:
105°+2y=180°
Now, we can solve for y:
1. Rearranging gives:
2y=180°−105°
2y=75°
2. Dividing by 2:
y=37.5°
Thus, the angle BDC is:
Angle BDC=37.5°
Topper's Solved these Questions
- POLYGONS AND QUADRILATERALS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALS EXERCISE - SELF ASSESSMENT SHEET - 23
10 Videos
- POLYGONS AND QUADRILATERALS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALS EXERCISE - SELF ASSESSMENT SHEET - 23
10 Videos
- PERCENTAGE AND ITS APPLICATIONSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERCENTAGE AND ITS APPLICATIONSEXERCISE - SELFT ASSESMENT SHEET (SECTION-C DISCOUNT )
10 Videos
- PROBABILITYBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - SELF ASSESSMENT SHEET -29
10 Videos
Similar Questions
Knowledge Check
ABCD is a rhombus such that ∠ACB=50∘. Then. ∠ADB= ?
A50∘B40∘C65∘D130∘In a cyclic quadrilateral ABCD, it is being given that ∠A=(x+y+10)∘,∠B=(y+20)∘,∠C=(x+y−30)∘and∠D=(x+y)∘. Then, ∠B ?
A70∘B80∘C100∘D110∘
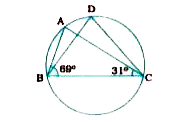
In the given figure ABCD is a quadrilateral ∠ADB=60∘,∠BAC=70∘,∠DBC=30∘,and∠ACB=60∘. Find ∠DACA30∘B40∘C50∘D60∘
ABCD is a rhombus such that ∠ACB=40∘. Find ∠ADB.
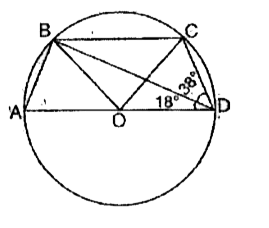
View SolutionAOD is a diameter of the circle with centre O. Given that ∠BDA=18∘and∠BDC=38∘.∠BCD equals
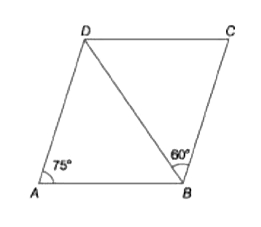
View SolutionIn the given figure, ABCD is a parallelogram in which ∠BAD=75∘and∠CBD=60∘. Then, ∠BDC is equal to
View SolutionQuestion Stimulus :-
Diagonal of a parallelogramABCD intersect at ). If ∠BOCm=90∘ and ∠BDC=50∘, then ∠OAB is equal to …..
View SolutionIn a circle with centre O, AOC is a diameter of the circle, BD is a chord and OB and CD are joined. If ∠AOB =130∘, then ∠BDC is equal to
View Solution