ABCD is a rectangle with ∠BAC=320. Determine ∠DBC.
To solve for the angle ∠DBC in rectangle ABCD where ∠BAC=32∘, we can follow these steps:
1. Understand the Properties of a Rectangle:
- In a rectangle, all angles are right angles, meaning each angle measures 90∘.
2. Identify the Given Angle:
- We are given ∠BAC=32∘.
3. Use the Properties of Angles in a Triangle:
- In triangle ABC, we can observe that:
- ∠ABC=90∘ (since it is a rectangle).
- ∠BAC=32∘ (given).
- Therefore, we can find ∠ACB using the fact that the sum of angles in a triangle is 180∘:
∠ACB=180∘−∠BAC−∠ABC
∠ACB=180∘−32∘−90∘=58∘
4. Relate ∠ACB to ∠DBC:
- Since ∠DBC and ∠ACB are alternate angles in the rectangle, we have:
∠DBC=∠ACB=58∘
5. Conclusion:
- Therefore, the measure of ∠DBC is 58∘.
Final Answer:
∠DBC=58∘
- In a rectangle, all angles are right angles, meaning each angle measures 90∘.
- We are given ∠BAC=32∘.
- In triangle ABC, we can observe that:
- ∠ABC=90∘ (since it is a rectangle).
- ∠BAC=32∘ (given).
- Therefore, we can find ∠ACB using the fact that the sum of angles in a triangle is 180∘:
∠ACB=180∘−∠BAC−∠ABC
∠ACB=180∘−32∘−90∘=58∘
- Since ∠DBC and ∠ACB are alternate angles in the rectangle, we have:
∠DBC=∠ACB=58∘
- Therefore, the measure of ∠DBC is 58∘.
∠DBC=58∘
Topper's Solved these Questions
Similar Questions
If ABCD is a rectangle with ∠BAC=32∘, find the measure of ∠DBC
View SolutionIn Fig. 32, ABCD is a rectangle of length AB=40 cm and breadth BC=25 cm. If P,Q,R,S be the mid-points of the sides AB, BC, CD and DA respectively, find the area of the shaded region.
View SolutionΔABC is isosceles with AB=AC. AD is the altitude from A on BC. Is ΔABD≅ΔACD? State the pairs of matching parts you have used to answer (i). Is it true to say that BD= DC?
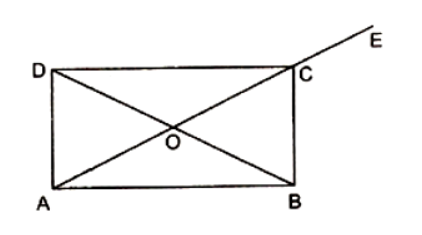
View SolutionIn Figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD=1460, find ∠AOB
View SolutionABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionIn Figure, ABCD is a parallelogram in which ∠DAO=400, ∠BAO=350 and ∠COD=650. Find: ∠ABO (ii) ∠ODC (iii) ∠ACB (iv) ∠CBD

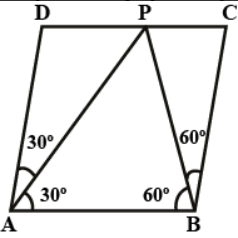
View SolutionIn Figure, ABCD is a parallelogram and ∠DAB=600. If the bisectors AP and BP of angles A and B respectively, meet at P on CD, prove that P is the mid-point of CD
View SolutionIn Figure, ABC is a triangle in which ∠B=2∠C . D is a point on side BC such that AD bisects ∠BAC and AB=CD.BE is the bisector of ∠B . The measure of ∠BAC is
(a) 720
(b) 730
(c) 740
(d) 960

View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC=35∘ , then ∠ABC= 70∘ (b) 110∘ (c) 90∘ (d) 120∘
View Solution

