In a rectangle ABCD, prove that ACB≅CAD.
To prove that triangle ACB≅CAD in rectangle ABCD, we will use the Angle-Angle-Side (AAS) congruence criterion. Here’s the step-by-step solution:
Step 1: Identify the Angles and Sides
In rectangle ABCD:
- ∠CAB and ∠DCA are alternate interior angles.
- ∠CBA and ∠ABC are both right angles (90 degrees).
Step 2: Establish Angle Relationships
1. Since ABCD is a rectangle, we know:
- ∠CBA=90∘ (as all angles in a rectangle are right angles).
- ∠ABC=90∘ (same reason).
2. Since ∠CAB and ∠DCA are alternate angles, we have:
- ∠CAB=∠DCA.
Step 3: Identify the Common Side
The side AC is common to both triangles ACB and CAD:
- AC=AC (common side).
Step 4: Apply the AAS Congruence Criterion
Now we have:
- ∠CAB=∠DCA (from step 2),
- ∠CBA=∠ABC=90∘ (from step 1),
- AC=AC (common side).
According to the AAS criterion, if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent.
Conclusion
Thus, we can conclude that:
△ACB≅△CAD
In rectangle ABCD:
- ∠CAB and ∠DCA are alternate interior angles.
- ∠CBA and ∠ABC are both right angles (90 degrees).
1. Since ABCD is a rectangle, we know:
- ∠CBA=90∘ (as all angles in a rectangle are right angles).
- ∠ABC=90∘ (same reason).
2. Since ∠CAB and ∠DCA are alternate angles, we have:
- ∠CAB=∠DCA.
The side AC is common to both triangles ACB and CAD:
- AC=AC (common side).
Now we have:
- ∠CAB=∠DCA (from step 2),
- ∠CBA=∠ABC=90∘ (from step 1),
- AC=AC (common side).
Thus, we can conclude that:
△ACB≅△CAD
Topper's Solved these Questions
Similar Questions
In the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that
(i) ar(ABCD)=ar(EFCD)
(ii) ar(ABCD)=DC×AL.
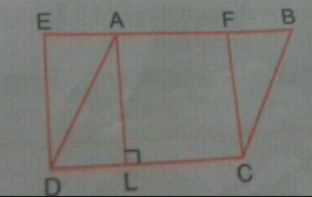
View SolutionABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that:
(i) ar (ABCD) = ar (EFCD)
(ii) ar (ABCD) = DC × AL
View SolutionIn Figure, ABCD is a parallelogram and EFCD is a rectangle. Also AL⊥DC. Prove that : ar(ABCD)=ar(EFCD) ar(ABCD)=DC×AL

View SolutionA paper is in the form of a rectangle ABCD in which AB=20 cm and BC=14 cm. A semicircular portion with BC as diameter is cut off. Find the area of the remaining part.
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
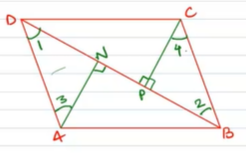
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
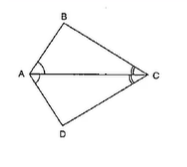
View SolutionABCD is a cyclic quadrilateral whose diagonals AC and BD intersect at P. If AB=DC, prove that:
(i)PAB ≅PDC
(ii)PA=PD and PC=PB (iii) AD∣∣BC
View SolutionIn Fig. 5.10, if AC=BD, then prove that AB=CD.

View Solution
