The diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
In rectangle ABCD diagonals meet at O.
in traingle ADO
∠BOC=∠AOD=44∘ [vertically opposite angle]
OA=OD[diagonals of a rectangle are equal and bisects each other]
so ∠OAD=∠ODA
now
∠OAD+∠ODA+∠OAD=180∘
∠OAD+∠ODA=180∘−44∘
∠OAD=68∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the length of diagonals of a rectangle AOBC whose three vertices are A(0, 3), O(0, 0) and B(5, 0).
A√23 unitsB5 unitsC√21 unitsD√34 units
The diagonals of a rectangle ABCD meet at O. If ∠BOC=44∘, find ∠OAD.
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=50∘ then find ∠ODA.
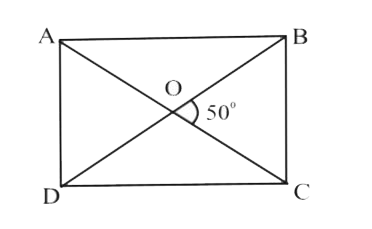
View SolutionThe diagonals of a parallelogram ABCD intersect at O . If ∠BOC=90∘ and ∠BDC=50∘, then ∠OAB= 40∘ (b) 50∘ (c) 10∘ (d) 900
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View SolutionThe diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in X and CD in Y. Show that ar(AXYD)=12(ARgmABCD)
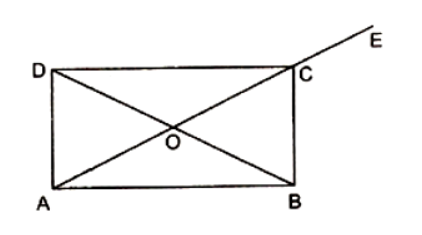
View SolutionIn Figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD=1460, find ∠AOB
View SolutionProve that the diagonals of quadrilateral ABCD,AC and BD intersect in O. Prove that if BO=OD, the triangles ABC and ADC are equal in area.
View Solution

