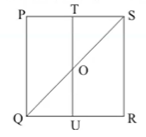
PQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
Given PQRS is a square and PR and SQ are diagonals.
we know that the diagonals of a square are bisecting each other at 900
so
∠POQ=900
Topper's Solved these Questions
Similar Questions
If PQRS is a square, then write the measure of ∠SRP
View SolutionIn Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that: PL=QM (ii) LO=OM
View SolutionABCD is a parallelogram whose AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar ( POA)= ar ( QOC).
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
View SolutionPQRS is a parallelogram. PXandQY are respectively, the perpendiculars from PandQ to SRandRS produced. Prove that PX=QY
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
View SolutionPQRS is a trapezium having PS a n d QR as parallel sides. A is any point on PQandB is a point on SR such that ABQR . If area of PBQ is 17cm2, find the area of ASR
View SolutionIn Figure, PSDA is a parallelogram in which PQ=QR=RS and APBQCR. Prove that ar ( PQE)= ar ( CFD).
View SolutionIf pqandrs are two rational number such that qands do not have a common factor other then 1 ie . HCF of qands is 1 then pq+rs=p×s+r×qq×s
View Solution

