In Fig. 5.10, if AC=BD, then prove that AB=CD.

AC=AB+BC
BD=BC+CD
BD=AB+BC
BC+CD=AB+BC
CD=AB
Hence Proved
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - INTRODUCTION TO EUCLIDS GEOMETRYEXERCISE - Exercise 5.22videos
INTRODUCTION TO EUCLIDS GEOMETRY
- BOOK - NCERTCHAPTER - INTRODUCTION TO EUCLIDS GEOMETRYEXERCISE - Solved Examples3videos
INTRODUCTION TO EUCLIDS GEOMETRY
- BOOK - NCERTCHAPTER - HERONS FORMULAEXERCISE - Solved Examples6videos
HERONS FORMULA
- BOOK - NCERTCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - EXERCISE 4.42videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
In Fig. 4.101, AD and CE are two altitudes of ABC . Prove that AEF~CDF (ii) ABD~CBE (iii) AEF~ADB (iv) FDC~BEC (FIGURE)
View SolutionIn Fig.108, if ABCD then the value of x is (a) 87 (b) 93 (c) 147 (d) 141
View SolutionIn Fig.109, If ABCD then the value of x is (a) 34 (b) 124 (c) 24 (d) 158
View SolutionIn Fig.112, if ABCD, then x= (a) 32 (b) 42 (c) 52 (d) 31
View SolutionIn Fig. 10.78, if AD, AE and BC are tangents to the circle at D, E and F respectively. Then, (FIGURE) AD=AB+BC+CA (b) 2AD=AB+BC+CA (c) 3AD=AB+BC+CA (d) 4AD=AB+BC+CA
View SolutionIn Fig.111, if ABCD then x= (a) 154 (b) 139 (c) 144 (d) 164
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
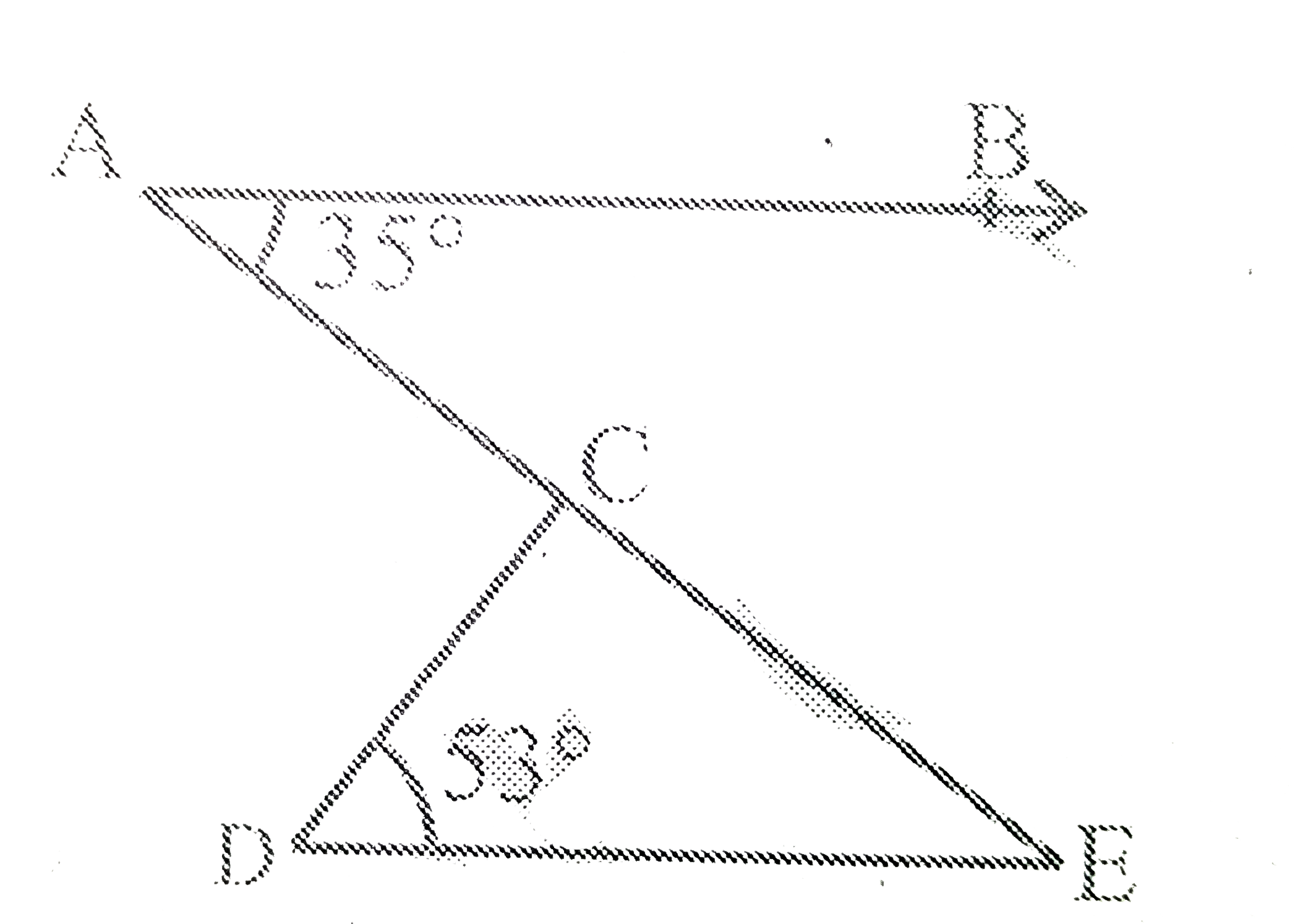 View Solution
View SolutionIn Fig. 4.179, ABC and DBC are on the same base BC . If AD and BC intersect at O , prove that Area (ABC)Area (DBC)=AODO (FIGURE)
View SolutionABCD is a cyclic quadrilateral whose diagonals AC and BD intersect at P. If AB=DC, prove that:
(i)PAB ≅PDC
(ii)PA=PD and PC=PB (iii) AD∣∣BCView SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View Solution

