Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
Given: ar(ΔAOD)=ar(ΔBOC)
To prove: ABCD is a trapezium.
Proof: ar(ΔAOD)=ar(ΔBOC)
⇒ar(ΔAOD)+ar(ΔAOB)=ar(ΔBOC)+ar(ΔAOB)
⇒ar(ΔADB)=ar(ΔACB)
Areas of ΔADB and ΔACB are equal.
Thus,They should be lying between the same parallel lines.
Hence AB∥CD
∴ ABCD is a trapezium.
Hence Proved.
Topper's Solved these Questions
Similar Questions
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(AOD)=ar(BOC) . Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each at P. Show That: ar(APB)×ar(CPD)=ar(APD)×ar(PBC)
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).

View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
View SolutionIf the diagonals AC,BD of a quadrilateral ABCD, intersect at O, and seqarate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram. GIVEN : A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) TO PROVE : Quadrilateral ABCD is a parallelogram.
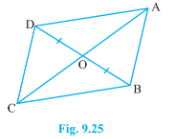
View SolutionIn Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:(i) ar (DOC) = ar (AOB)(ii) ar (DCB) = ar (ACB)(iii) D A\ ||\ C
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
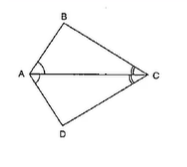
View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
View SolutionIf the bisectors of two adjacent angles A and B of a quadrilateral ABCD intersect at a point O such that ∠C+∠D=k∠AOB, then find the value of k
View SolutionIn a ABC , If LandM are points on ABandAC respectively such that LMparallel BC
Prove that: ar(LOB)=ar(MOC)
View Solution
