In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:(i) ar (DOC) = ar (AOB)(ii) ar (DCB) = ar (ACB)(iii) D A\ ||\ C
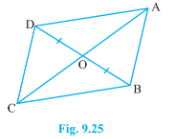
We can draw a perpendicular from vertices B and D on diagonal AC which will help us to make congruent triangles and we know that congruent triangles are always equal in areas.
If two triangles have the same base and also have equal areas, then these triangles must lie between the same parallels.
Let us construct DN⊥AC and BM⊥AC.
i) In △DON and △BOM,∠DNO=∠BMO=90∘ (By construction)
∠DON=∠BOM (Vertically opposite angles are equal)
OD=OB (Given)
By AAS congruence rule, △DON≅△BOM
DN=BM (By CPCT)
... (1)
We know that congruent triangles have equal areas.
Area(△DON)=Area(△BOM) ...(2)
Now, In △DNCand△BMA,
∠DNC=∠BMA=90∘ (By construction)
CD=AB
(given)DN=BM [Using Equation (1)]
△DNC≅△BMA (RHS congruence rule)
Area(△DNC)=Area(△BMA) ... (3)
On adding Equations (2) and (3), we obtainar(△DON)+ar(△DNC)=ar(△BOM)+ar(△BMA)
Therefore, Area(△DOC)=Area(△AOB)
ii) We obtained,Area(△DOC)=Area(△AOB)
Now, adding Area(△OCB) to both sides
ar(△DOC)+ar(△OCB)=ar(△AOB)+ar(△OCB)
Area(△DCB)=Area(△ACB)
iii) We obtained,Area(△DCB)=Area(△ACB)
If two triangles are having the same base and also having equal areas, then these triangles must be lie between the same parallels.
DA∣∣CB ... (4)
In quadrilateral ABCD, one pair of opposite sides are equal (AB=CD) and the other pair of opposite sides are parallel(DA∣∣CB).
Therefore, ABCD is a parallelogram.
Similar Questions
In Fig 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.If AB=CD , then show that
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(AOD)=ar(BOC) . Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each at P. Show That: ar(APB)×ar(CPD)=ar(APD)×ar(PBC)
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
View SolutionIf the bisectors of two adjacent angles A and B of a quadrilateral ABCD intersect at a point O such that ∠C+∠D=k∠AOB, then find the value of k
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).

View SolutionIf ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
View SolutionThe diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in X and CD in Y. Show that ar(AXYD)=12(ARgmABCD)
View SolutionThe diagonals of quadrilateral ABCD,ACandBD intersect in O. Prove that if BO=OD, the triangles ABCandADC are equal in area.
View Solution
