Diagonals AC and BD of a quadrilateral ABCD intersect each at P. Show That: ar(APB)×ar(CPD)=ar(APD)×ar(PBC)
We know that,
Area of a Δ is (1/2)*base*height.
So with reference to the figure,
Ar(ΔAPD)=(12)⋅x⋅DP...................(1)
Ar(ΔBPC)=(12)⋅y⋅BP..................(2)
Since height for ΔAPB is x and for ΔCPD is y
So Ar(ΔAPB)=(12)⋅x⋅BP...................(3)
Ar(ΔAPD)=(12)⋅y⋅DP..................(4)
Thus from (1),(2),(3) and (4),
Ar(ΔAPD)*Ar(ΔBPC)=Ar(ΔAPB)*Ar(ΔAPD)
Topper's Solved these Questions
Similar Questions
Diagonals AC and BD of a quadrilateral ABCD intersect each at P. Show That: ar(APB)×ar(CPD)=ar(APD)×ar(PBC)
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(AOD)=ar(BOC) . Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of □ABCD intersect each other at point P. Show that ar(△APB)×ar(△CPD)=ar(△APD)×ar(△BPC)
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
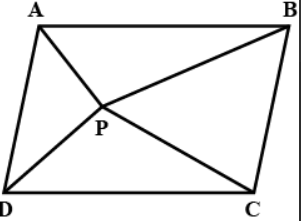
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)

View SolutionThe diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD=50∘, then ∠DPC= 70∘ (b) 90∘ (c) 80∘ (d) 100∘
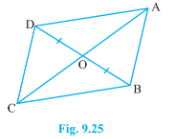
View SolutionIn Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:(i) ar (DOC) = ar (AOB)(ii) ar (DCB) = ar (ACB)(iii) D A\ ||\ C
View SolutionIn a quadrilateral ABCD, P and Q are mid-ponts. Show that ar(AXD)+ar(BYC)=ar(PXQY)
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View Solution