Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
Let us draw a point X and N on BD such that
AN⊥BD and CX⊥BD.
Then,
L.H.S.=ar(APB)×ar(CPD)
12(AN)(PB)×12(CX)(PD)
12(AN)(PD)×12(CX)(PB)
ar(APD)×ar(BPC)=R.H.S.
Similar Questions
Knowledge Check
The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then,it is always true that
AAP. CP = BP. DPBAP.BP = CP. DPCAP. CD = AB. CPDBP. AB = CD.CPIf bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D at R and of ∠Dand∠A at S then PQRS is a
ArectangleBparallelogramCrhombusDquardilateral whose opposite angles are supplementary
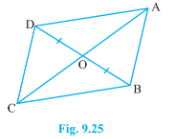
In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:(i) ar (DOC) = ar (AOB)(ii) ar (DCB) = ar (ACB)(iii) D A\ ||\ C
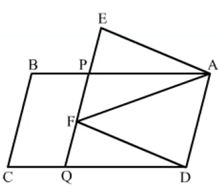
View SolutionIn Figure, ABCDandAEFD are two parallelograms? Prove that: ar(APE):ar(PFA)=ar(QFD):ar(PFD)
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)

View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View SolutionIf the diagonals AC,BD of a quadrilateral ABCD, intersect at O, and seqarate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram. GIVEN : A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) TO PROVE : Quadrilateral ABCD is a parallelogram.
View SolutionABCD is a cyclic quadrilateral whose diagonals ACandBD intersect at P . If AB=DC, Prove that : PAB≅PDC PA=PDandPC=PB ADBC
View Solution
