A point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the other pair of triangles. Given: A rectangle ABCDandO is a point inside it. OA,OB,OCandOD have been joined. To Prove: ar(AOD)+ar(BOC)=ar(AOB)+ar(COD)
Given: A rectangle ABCD and O is a point inside it. OA, OB, OC and OD have been joined.
To prove: ar(△AOD)+ar(△BOC)=ar(△AOB)+ar(△COD).
Construction: Draw EOF∣∣AB and LOM∣∣AD.
Proof: EOF∣∣AB and DA cuts them.
∴∠DEO=∠EAB=90∘(corresponding /_).
∴OE⊥AD.
Similarly, OF⊥BC, OL⊥AB and OM⊥DC.
∴ar(△AOB)+ar(△BOC)
=(12×AD×OE)+(12×BC×OF)
=12AD×(OE+OF) [∴BC=AD]
=12×AD×EF=12×AD×AB [∴EF=AB]
=12×ar(rec.ABCD).
Again, ar(△AOB)+ar(△COD)
=(12×AB×OL)+(12×DC×OM)
=12×AB×(OL+OM) [∴DC=AB]
=(12×AB×OL)+(12×DC×OM)
=12×AB×(OL+OM)
=12×ar(rect.ABCD).
∴ar(△AOD)+ar(△BOC)=ar(△AOB)+ar(△COD).
Topper's Solved these Questions
Similar Questions
A point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the other pair of triangles. GIVEN : A rectangle ABCD and O is a point inside it. OA,OB,OC and OD have been joined.. TO PROVE : ar(AOD)+ar(BOC)=ar(AOB)+ar(COD) CONSTRUCTION : Draw EOFAB and LOMAD.
View SolutionThe vertices of a rectangle PQRS are joined from an interior point 'O'. Prove that the sum of the area of two opposite triangles so formed is equal to the sum of the areas of remaining two triangles
View SolutionIn Figure, ABCD is a parallelogram O s any point on AC, PQparallelAB and LMparallelAD
Prove that ar(parallelogram)DLOP)=ar(parallelogram BMOQ)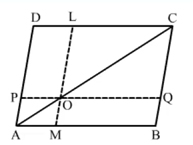
View SolutionIn a ABC , If LandM are points on ABandAC respectively such that LMparallel BC
Prove that: ar(LOB)=ar(MOC)
View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).

View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area. GIVEN : A parallelogram ABCD . The diagonals AC and BD intersect at O. TO PROVE : ar(OAB)=ar(OBC)=ar(OCD)=ar(AOD)
View SolutionThe diagonals of quadrilateral ABCD,ACandBD intersect in O. Prove that if BO=OD, the triangles ABCandADC are equal in area.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View Solution

