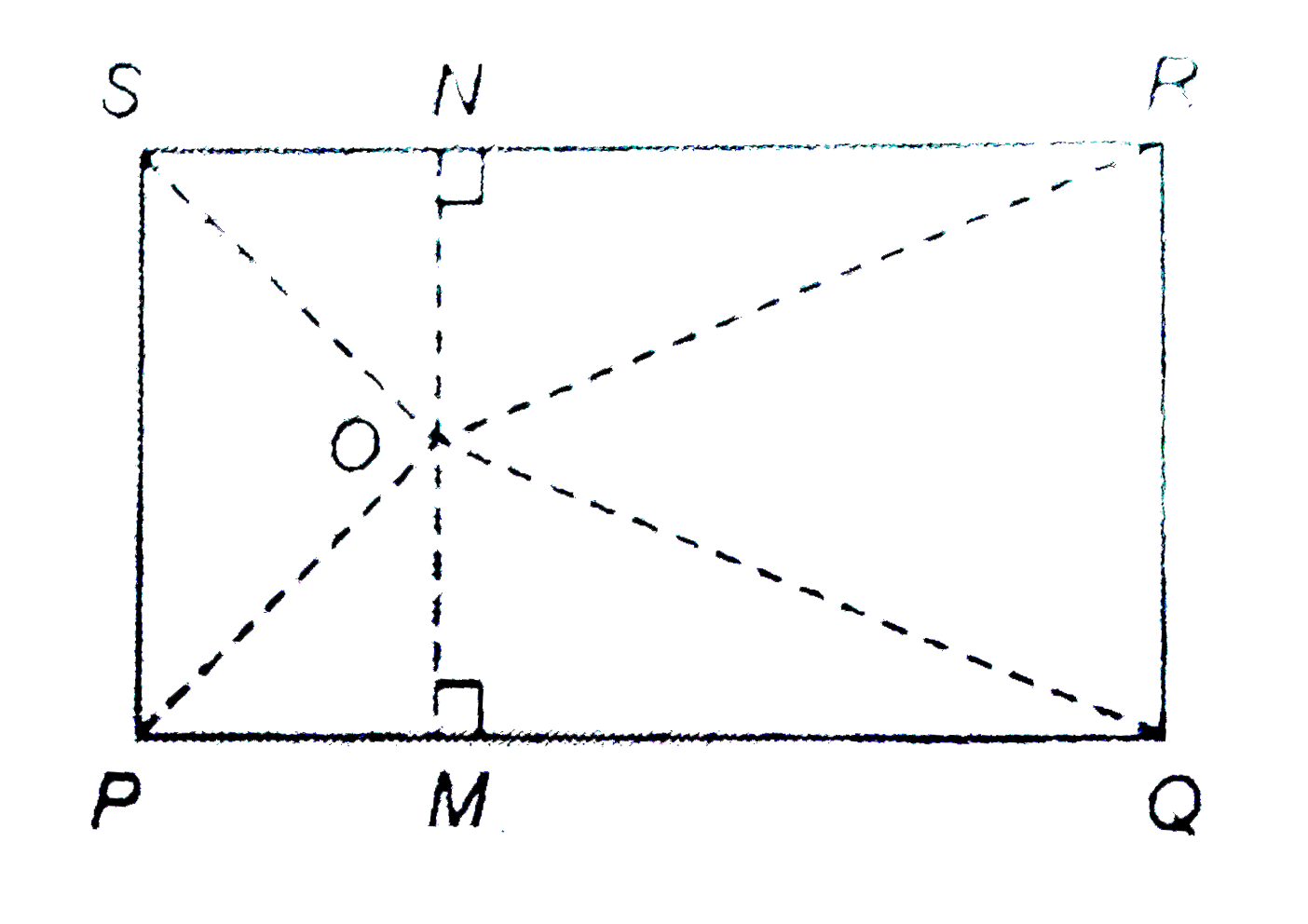
The vertices of a rectangle PQRS are joined from an interior point 'O'. Prove that the sum of the area of two opposite triangles so formed is equal to the sum of the areas of remaining two triangles

Video Solution

Text Solution

Verified by Experts

Through O, draw $M N ⊥ P Q$
$∴$ area of $Δ O P Q + area of Δ O R S$
$= \frac{1}{2} \times P Q \times O M + \frac{1}{2} \times R S \times O N$
$= \frac{1}{2} \times P Q \times O M + \frac{1}{2} \times P Q \times O N$
( $∴ R S = P Q$ , opposite sides of a rectangle)
$= \frac{1}{2} \times P Q \times (O M + O N) = \frac{1}{2} \times P Q \times M N$
$= \frac{1}{2} \times P Q \times Q R = \frac{1}{2} \times$ area of rectangle PQRS ....(1)
Again
area of $Δ O P S + area of Δ O Q R = area of □ P Q R S - (area of Δ O P Q + area of Δ O R S)$
= area of $□ P Q R S - \frac{1}{2} \times$ area of $□ P Q R S$ [from (1)]
$= \frac{1}{2} \times area of □ P Q R S$ ...(2)
From (1) and (2), we get.
area of $Δ O P Q + area of Δ O R S = area of Δ O P S + area of Δ O Q R$

Updated on:21/07/2023

|

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
Aan isosceles triangle
Ban obtuse triangle
Can equilateral triangle
Da right triangle
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
Aan isosceles triangle
Ban obtuse triangle
Can equilateral triangle
Da right triangle

NAGEEN PRAKASHAN-AREA OF PARALLELOGRAMS AND TRIANGLES-Revision Exercise (long Answer Question)

Home
Ask Doubt
Profile