O is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(OAB)=ar(OBC)
Given: O is any point on the diagonal BD of the parallelogram ABCD
To prove: ar(△OAB)=ar(△OBC)
Proof: Join AC, which intersects BD at P. Since the diagonals of a parallelogram bisect each other.
∴P is the mid-point of both AC and BD.
Now,
In △ABC, BP is the median.
∴ar(△ABP)=ar(△CBP).......(1)
In △OAC, OP is the median.
∴ar(△OAP)=ar(△OCP) ......(2)
On adding equation (1) and equation (2), we get:
ar(△ABP)+ar(△OAP)=ar(△CBP)+ar(△OCP)
⇒ar(△OAB)=ar(△OBC).
Topper's Solved these Questions
Similar Questions
P and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
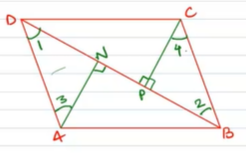
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
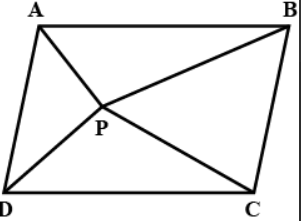
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)

View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
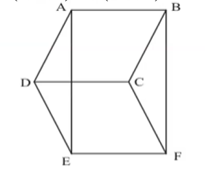
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
View SolutionA point D is taken on the side BC of a ABC such that BD=2DC. Prove that ar ( ABD)= 2 ar ( ADC)
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).

View SolutionIn Figure, ABCD is a parallelogram O s any point on AC, PQparallelAB and LMparallelAD
Prove that ar(parallelogram)DLOP)=ar(parallelogram BMOQ)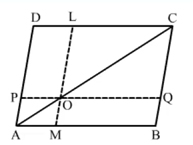
View Solution