Any point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
Proof : InΔABE, Side is having BD (As a Median)
Now, ar(ΔBED) = ar(ΔBAD) [Median of a Δ divides it into 2 Δ's of equal areas] ...(1)InΔACE, Side AE is having CD (As Median).
Now, ar(ΔECD) = ar(ΔACD) [Median of a Δ divides it into 2 Δ's of equal areas] ...(2)
adding (1) and (2), we get
ar(ΔBED) + ar(ΔECD)=
ar(ΔBAD) + ar(ΔACD)
⇒ar(ΔBEC) = ar(ΔABC)
Topper's Solved these Questions
Similar Questions
D is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE, prove that ar ( BOE)=18ar ( ABC)
View SolutionIn Figure DandE are two points on BC such that BD=DE=EC Show that ar(ABD)=ar(ADE)=ar(AEC)
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).

View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionBD is one of the diagonals of a quadrilateral ABCD. AM and CN are the perpendiculars from A and C , respectively, on BD. Show That ar (qua..ABCD)=12BD.AM+CN
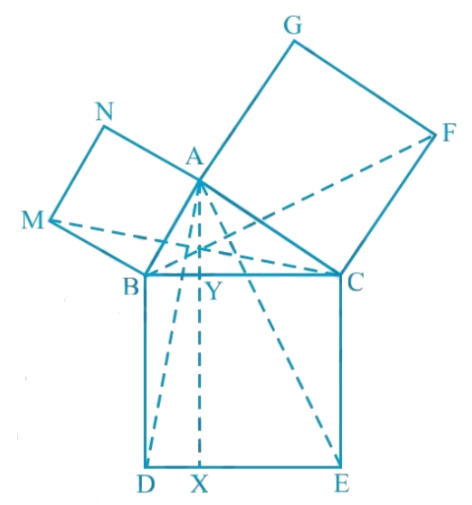
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=2 ar ( MBC)
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View SolutionP is any point on base BC of ABC and D is the mid-point of BC.DE is drawn parallel to PA to meet AC at E. If ar(ABC)=12cm2 , then find area of EQC
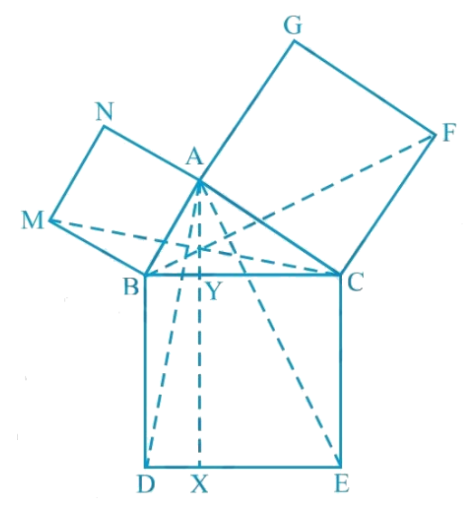
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)=2ar( FCB)
View Solution

