ABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of BED=14areaofABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(BED)=14ar(ABC).
Proof:
Since AD is the median of ΔABC, so it will divide ΔABC into two equal triangles.
∴ar(ΔABD)=ar(ΔADC)
Also, ar(ΔABD)=12ar(ABC) .....(i)
Now, InΔABD, BE is the median,
Therefore, BE will divide ΔABD into two equal triangles.
ar(ΔBED)=ar(ΔBAE) and ar(ΔBED)=12ar(ΔABD)
ar(ΔBED)=12×[12ar(ABC)] (Using equation (i))
∴ar(ΔBED)=14ar(ΔABC)
Hecne Proved.
Topper's Solved these Questions
Similar Questions
D is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE, prove that ar ( BOE)=18ar ( ABC)
View SolutionABC is a triangle in which D is the mid-point of BC ,E andF are mid-points of DC and AE respectively. If area of ABC is 16cm2, find the area of DEF
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
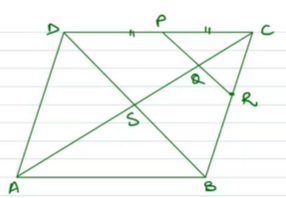
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionIf B is the mid point of ACandC is the mid point of BD,whereA,B,C,D lie on a straight line, say why AB=CD?
View Solution
