ABC is a right-angled triangle and O is the mid-point of the side oppo

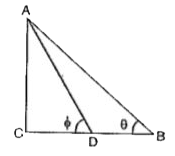
ABC is right angled triangle, right angled at C . D is the midpoint of BC. Then , $\frac{tan θ}{tan ϕ}$ =

A1
B $\frac{1}{\sqrt{2}}$
C $\frac{1}{2}$
D2
If ABC is a right angled triangle at B and M, N are the mid-points of AB and BC, then $4 (A N^{2} + C M^{2})$ is equal to :
A $4 A C^{2}$
B $6 A C^{2}$
C $5 A C^{2}$
D $\frac{5}{4} A C^{2}$
a and b are two side adjacent to the right angle of a right-angled triangle and p is the perpendicular drawn to the hypotenuse from the opposite vertex. Then $p^{2}$ is equal to
A $a^{2} + b^{2}$
B $\frac{1}{a^{2}} + \frac{1}{b^{2}}$
C $\frac{a^{2} b^{2}}{a^{2} + b^{2}}$
D $a^{2} - b^{2}$

ABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C.