If S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
Video Solution
Text Solution
Clearly, by triangle law of addition, we have

PQ+QS=PS . . . (i)
and PR+RS=PS . . . (ii)
On adding Eqs. (i) and (ii), we get
(PQ+QS)+(PR+RS)=2PS
⇒(PQ+PR)+(QS+RS)=2PS
⇒PQ+PR+0=2PS
[∵ S is mid-point of QR∴QS=−RS]
Hnce, PQ+PR=2PS Hence, proved.
|
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 1
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 2
Explore 17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
Knowledge Check
If S is any point on the side QR of a ΔPQR, then
APQ+QR+RP>2PSBPQ+QR+RP<2PSCPQ+QR+RP=3PSDNone of theseIf S is a point on side PQ of a ΔPQR such that PS=QS=RS, then
APR⋅QR=RS2BQS2+RS2=QR2CPR2+QR2=PQ2DPS2+RS2=PR2
S in any point on side QR of a ΔPQR.ShowtˆPQ + QR+RP gt 2PS.
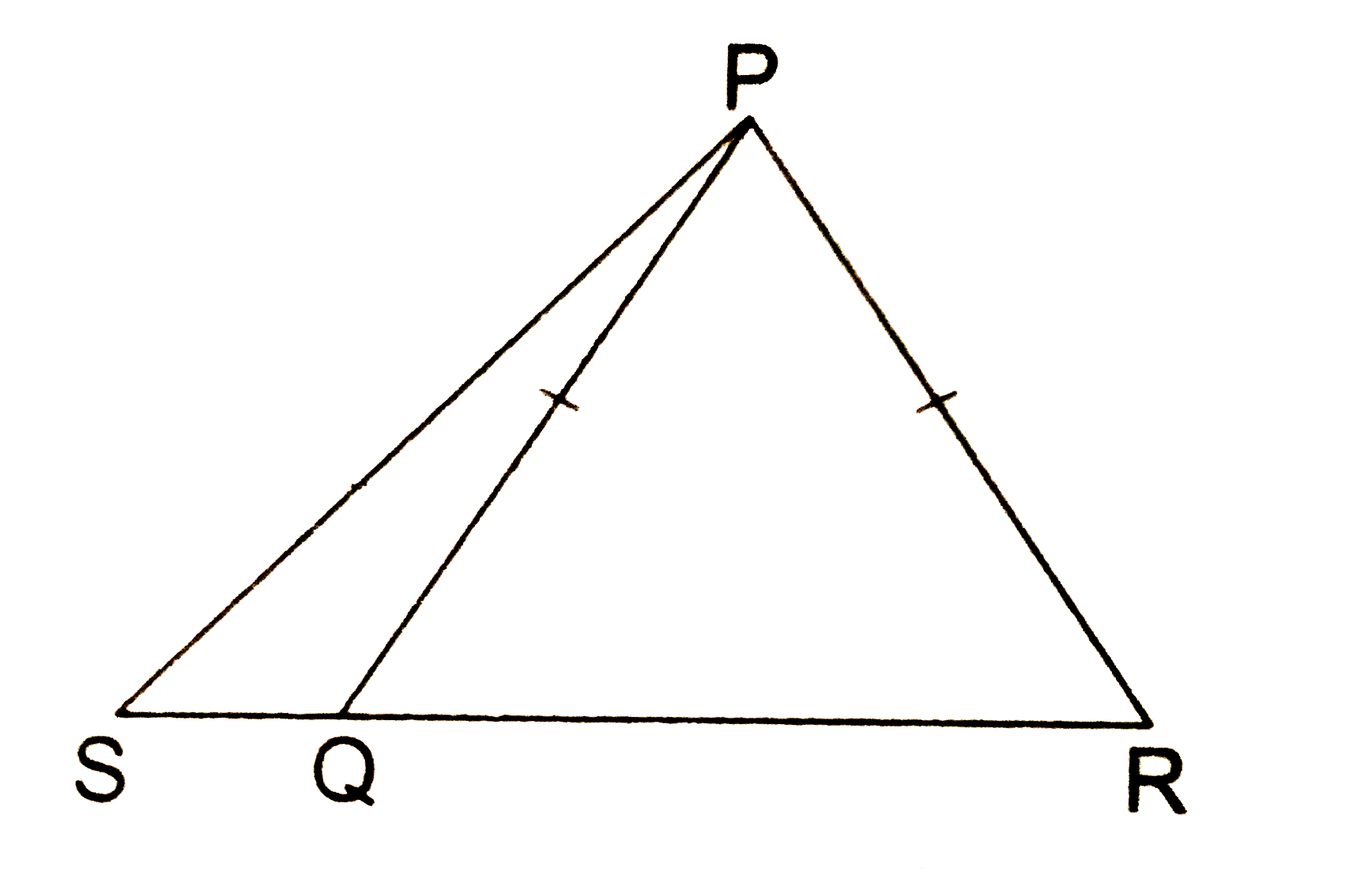
View SolutionIf Q is a point on the side SR of a triangle PSR such that PQ=PR then prove that PS>PQ
View SolutionIn the given figure, Q is a point on the side SR of ΔPSR such that PQ = PR. Prove that PS>PQ.
View SolutionIf S is a point on side PQ of a △PQR such that PS = QS = RS, then PR2+QR2 = ……………..
View Solution□PQRS is a reactangle. If A, B and C are the mid-points of PQ, PS and QR respectively, then prove that
AB+AC=12(PR+SQ).
View SolutionIn the figure given below PS is the bisector of ∠QPR of ΔPQR . Prove that QSSR=PQPR .

View Solution