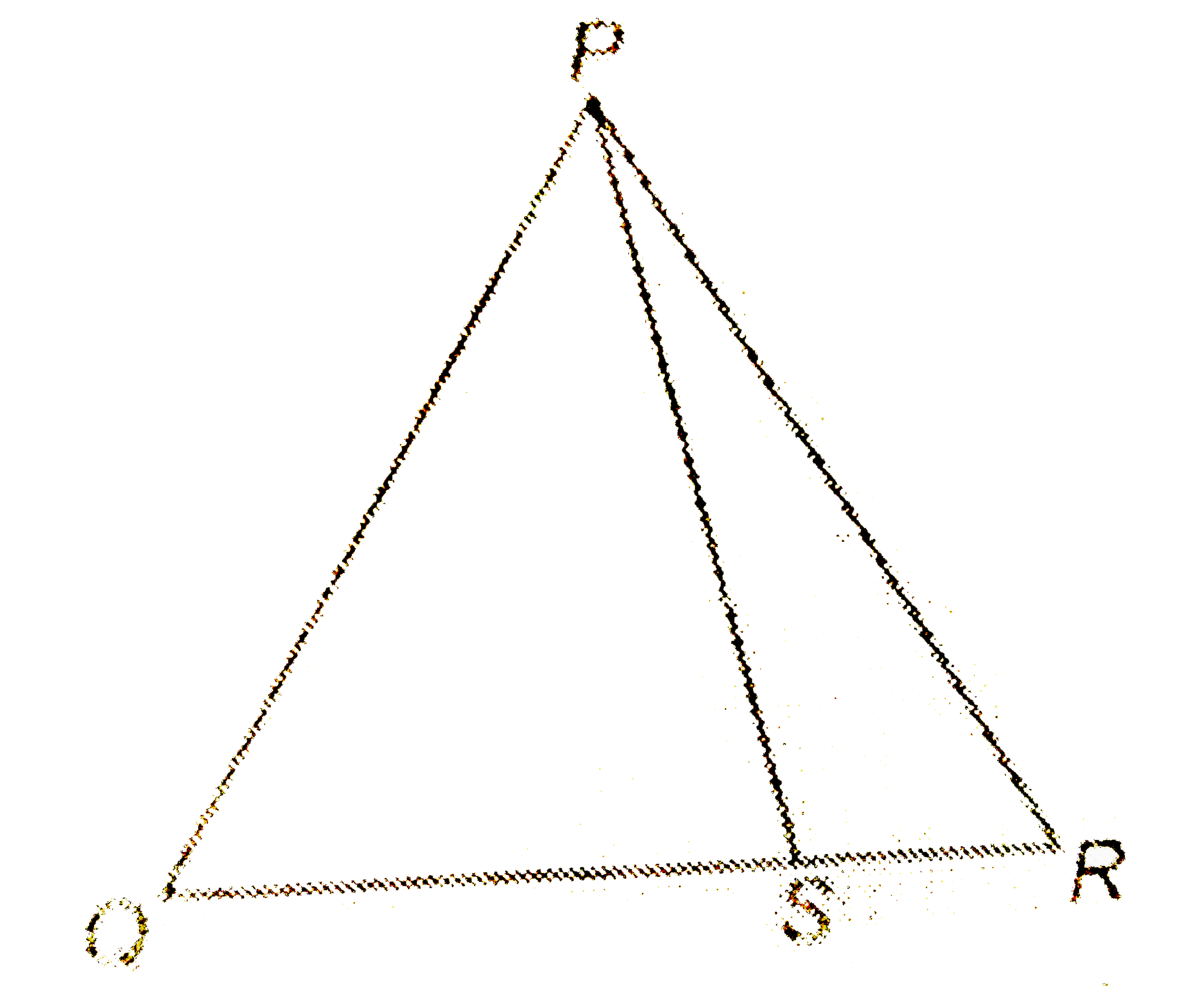
S is any point on side QR of a $Δ P Q R$ . Show that $P Q + Q R + R P > 2 P S$ .

Video Solution

Text Solution

Verified by Experts

Given : A point S on side QR of $Δ P Q R$ .
Tp prove : $P Q + Q R + R P > 2 P S$
Proof : In $Δ P Q S$ , we have
$P Q + Q S > P S$ ...(1)
( $∵$ sum of any sides of a triangle is greater than the third side)
Now, in $Δ P S R$ , we have
$R S + R P > P S$ ...(2)
( $∵$ Sum of any two sides of a triangle is greater than the third side)
Adding (1) and (2), we get
$P Q + Q S + R S + R P > 2 P S$
$\Rightarrow P Q + Q R + R P > 2 P S$

|

Updated on:21/07/2023

Class 9 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If S is any point on the side QR of a $Δ P Q R$ , then
A $P Q + Q R + R P > 2 P S$
B $P Q + Q R + R P < 2 P S$
C $P Q + Q R + R P = 3 P S$
DNone of these
Question 2 - Select One
If S is a point on side PQ of a $Δ P Q R$ such that PS=QS=RS, then
A $P R \cdot Q R = R S^{2}$
B $Q S^{2} + R S^{2} = Q R^{2}$
C $P R^{2} + Q R^{2} = P Q^{2}$
D $P S^{2} + R S^{2} = P R^{2}$
Question 3 - Select One
S and U are two points on the side PQ of $Δ P Q R$ , such that QU=PS . If ST||QR and $U V ∣ ∣ P R$ , then
ATV||PQ
B $T V ⊥ P Q$
CTV and PQ intersect at $60^{\circ}$
DTV and PQ intersect at $45^{\circ}$

NAGEEN PRAKASHAN-TRIANGLES-Revision Exercise (long Answer Type Question)

Home
Ask Doubt
Profile