In PQR
, S
is any point on the
side QR
. Show that PQ+QR+RP>2PS
To prove that PQ+QR+RP>2PS for triangle PQR with point S on side QR, we can follow these steps:
1. Identify the Triangle and Points:
Let's consider triangle PQR with points P, Q, R, and point S located on side QR.
2. Apply the Triangle Inequality:
According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle is greater than the length of the third side. We will apply this theorem to triangles PQS and PRS.
3. Triangle PQS:
For triangle PQS:
PQ+QS>PS(1)
4. Triangle PRS:
For triangle PRS:
PR+SR>PS(2)
5. Add the Inequalities:
Now, we add inequalities (1) and (2):
(PQ+QS)+(PR+SR)>PS+PS
This simplifies to:
PQ+QS+PR+SR>2PS
6. Substitute QR:
Notice that QS+SR=QR (since S is on line segment QR). Therefore, we can replace QS+SR with QR:
PQ+QR+PR>2PS
7. Conclusion:
We have shown that:
PQ+QR+RP>2PS
This completes the proof.
Let's consider triangle PQR with points P, Q, R, and point S located on side QR.
According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle is greater than the length of the third side. We will apply this theorem to triangles PQS and PRS.
For triangle PQS:
PQ+QS>PS(1)
For triangle PRS:
PR+SR>PS(2)
Now, we add inequalities (1) and (2):
(PQ+QS)+(PR+SR)>PS+PS
This simplifies to:
PQ+QS+PR+SR>2PS
Notice that QS+SR=QR (since S is on line segment QR). Therefore, we can replace QS+SR with QR:
PQ+QR+PR>2PS
We have shown that:
PQ+QR+RP>2PS
This completes the proof.
Topper's Solved these Questions
Similar Questions
In Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
View SolutionIn Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
View SolutionPQRS is a trapezium having PS a n d QR as parallel sides. A is any point on PQandB is a point on SR such that ABQR . If area of PBQ is 17cm2, find the area of ASR
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.

View SolutionIf PQRS is a square, then write the measure of ∠SRP
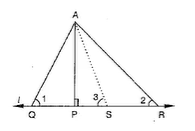
View SolutionIn Figure, AP ⊥l and PR>PQ . Show that AR>AQ Given: AP⊥l and PR>PQ To Prove: AR>AQ Construction: Mark a point S on PR such that PS=PQ. Join AS
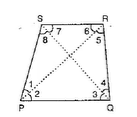
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

View Solution

