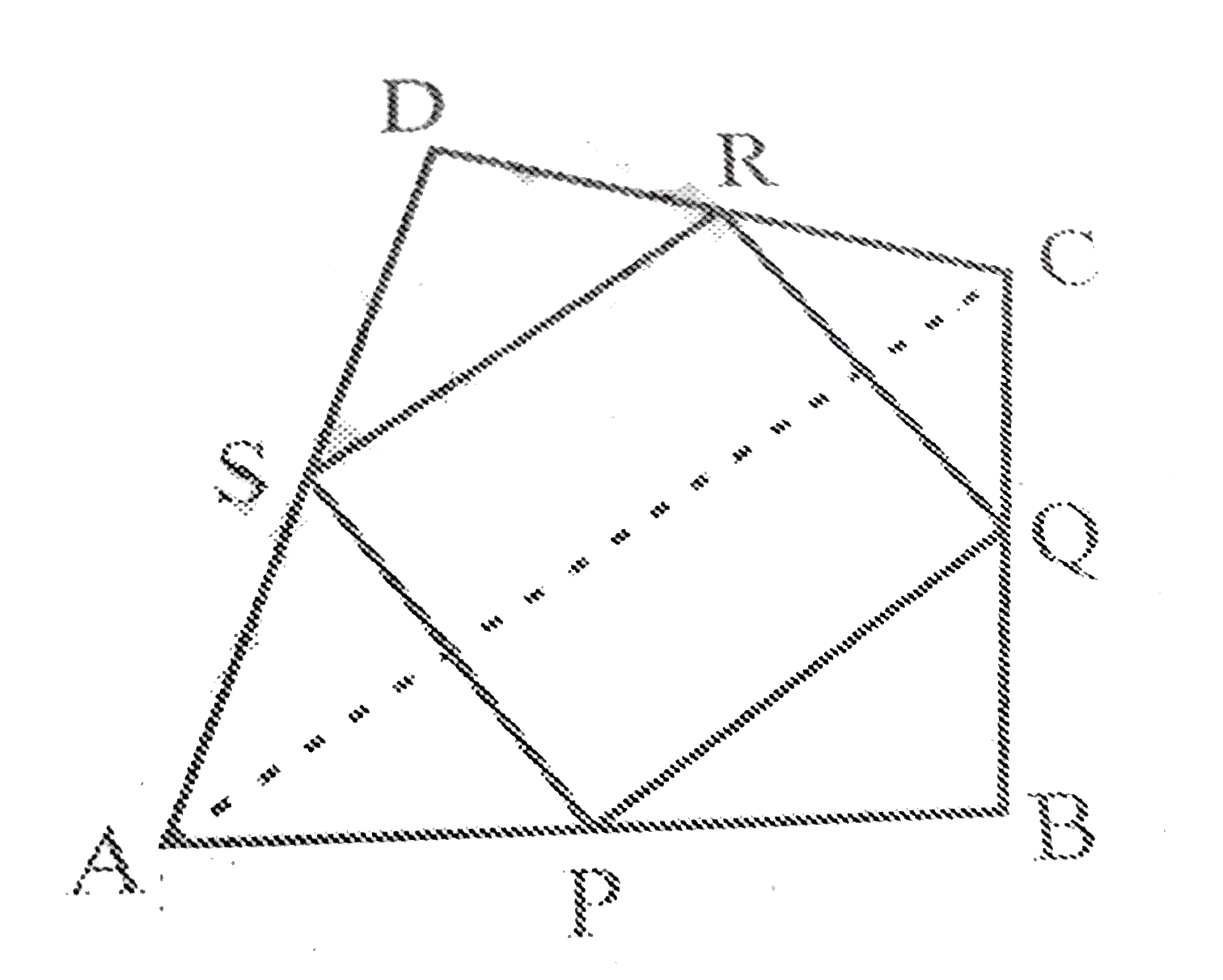
Prove that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
Given: In quadrilateral ABCD
P,Q,R and S are the midpoints of sides AB,BC,CD and DA
AC is the diagonal
To prove: PQRS is a parallelogram
Proof: (i) In △ABC,
P and Q are the mid-points of AB and BC
PQ parallel to AC and PQ=12AC ..(ii) [Using the mid point theorem ]
(i)In △ADC,
S and R are the mid-point of AD and DC
SR parallel to AC and SR=12AC ...(ii) [ Using the mid point theorem ]
(iii)Using equation (i) and (ii), We get:
PQ=SR and PQ parallel to SR
(iv)∴PQRS is a parallelogram.
Hence proved.
Topper's Solved these Questions
Similar Questions
Prove that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
(i) SR ∣∣ ACand SR=12AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
View SolutionABCD is a rhombus and P,Q,R,S are the mid-points of AB,BC,CD,DA respectively. Prove that PQRS is a rectangle.
View SolutionABCD is a quadrilateral; P,Q,RandS are the points of trisection of side AB,BC,CDandDA respectively and are adjacent to AandC ; prove that PQRS is parallelogram.
View SolutionIn Fig. 32, ABCD is a rectangle of length AB=40 cm and breadth BC=25 cm. If P,Q,R,S be the mid-points of the sides AB, BC, CD and DA respectively, find the area of the shaded region.
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
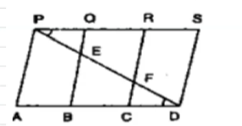
View SolutionIn Figure, PSDA is a parallelogram in which PQ=QR=RS and APBQCR. Prove that ar ( PQE)= ar ( CFD).
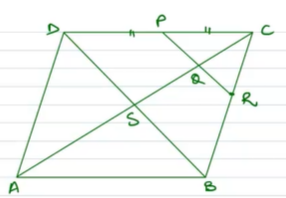
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
View Solution
