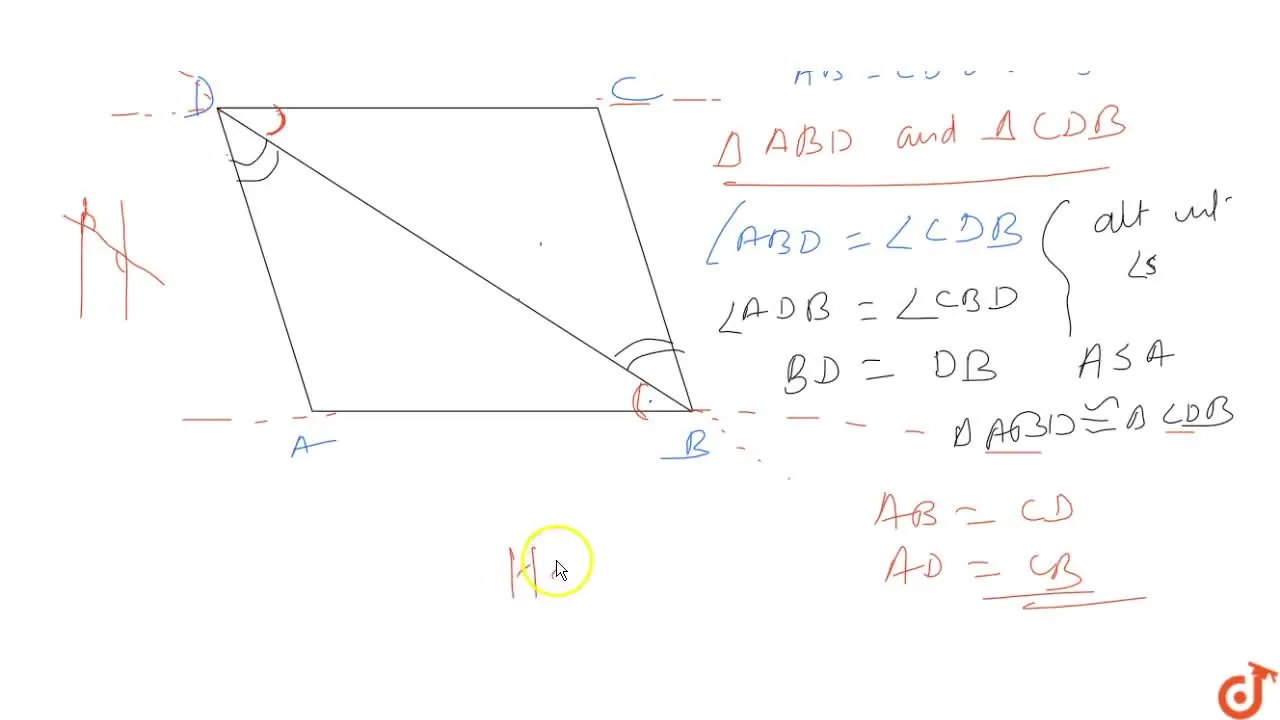
Prove that In a parallelogram, opposite side are equal
In △ADC and △ABC
∠DAC=∠ACB (AB parallel CD and taking AC as transversal)
AC=AC (common)
∠DCA=∠BAC (AB parallel CD taking AC as transversal)
By ASA criterion of concurrency △ADC is congruent to △ABC.
AD=BC (By CPCT)
AB=CD (By CPCT)
Hence, proved that in a parallelogram, opposite side are equal.
Related Playlists
Similar Questions
In a parallelogram opposite sides are equal
View SolutionProve that In a parallelogram, opposite sides are equal.
View SolutionProve that in a parallelogram, opposite angles are equal.
View SolutionA quadrilateral is a parallelogram if its opposite sides are equal.
View SolutionAssertion: Every rectangle is a parallelogram.
Reason: Rectangle satisfies all the properties of parallelogram as opposite sides are equal and parallel, diagonals biseect each other and opposite angles are equal.View SolutionA quadrilateral is parallelogram if its opposite sides are equal
View SolutionProve that of all parallelograms of which the sides are given, the parallelogram which is rectangle has the greatest area.
View SolutionIs quadrilateral ABCD a parallelogram?
I. Its opposite sides are equal.
II. Its opposite angles are equal.
The correct answer is : (a) /(b)/(c )/(d).View SolutionUsing dot product of vectors; prove that a parallelogram; whose diagonal are equal; is a rectangle.
View SolutionFor two statement p and q
p : A quadrilateral is a parallelogram
q : The opposite sides are parallel
Then, the compound proposition, ''A quadrillateral is a parallelogram if and only if the opposite sides are parallel'' is represented byView Solution