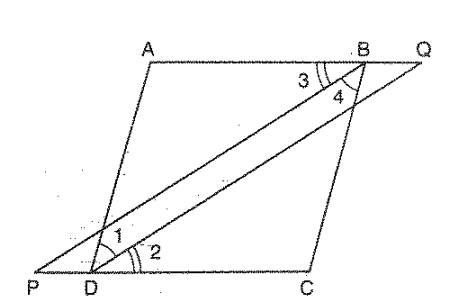
In Figure, bisectors of and of quadrilateral meet and produced at Q respectively. Prove that :
To prove that ∠P+∠Q=12(∠ABC+∠ADC), we will follow these steps:
Step 1: Analyze Triangle PBC
In triangle PBC, we know that the sum of angles is 180∘. Therefore, we can write:
∠CPB+∠PBC+∠BCP=180∘
Let ∠CPB=∠P and ∠PBC=12∠ABC (since BP is the bisector of ∠ABC). Thus, we can rewrite the equation as:
∠P+12∠ABC+∠BCP=180∘(1)
Step 2: Analyze Triangle QAD
Similarly, in triangle QAD, we can also apply the angle sum property:
∠AQR+∠QAD+∠DAQ=180∘
Let ∠AQR=∠Q and ∠QAD=12∠ADC (since DQ is the bisector of ∠ADC). Thus, we can rewrite this equation as:
∠Q+12∠ADC+∠DAQ=180∘(2)
Step 3: Add the Two Equations
Now, we will add equations (1) and (2):
(∠P+12∠ABC+∠BCP)+(∠Q+12∠ADC+∠DAQ)=180∘+180∘
This simplifies to:
∠P+∠Q+12∠ABC+12∠ADC+∠BCP+∠DAQ=360∘
Step 4: Relate to Quadrilateral ABCD
Since ABCD is a quadrilateral, the sum of its angles is 360∘:
∠A+∠B+∠C+∠D=360∘
Thus, we can equate:
∠BCP+∠DAQ=∠A+∠C
Step 5: Substitute Back
Substituting ∠BCP+∠DAQ into our previous equation, we get:
∠P+∠Q+12∠ABC+12∠ADC+∠A+∠C=360∘
Now, since ∠A+∠C=360∘−(∠ABC+∠ADC):
∠P+∠Q+12∠ABC+12∠ADC+(360∘−(∠ABC+∠ADC))=360∘
Step 6: Simplify
This simplifies to:
∠P+∠Q+12∠ABC+12∠ADC=180∘
Rearranging gives us:
∠P+∠Q=12(∠ABC+∠ADC)
Conclusion
Thus, we have proved that:
∠P+∠Q=12(∠ABC+∠ADC)
In triangle PBC, we know that the sum of angles is 180∘. Therefore, we can write:
∠CPB+∠PBC+∠BCP=180∘
Let ∠CPB=∠P and ∠PBC=12∠ABC (since BP is the bisector of ∠ABC). Thus, we can rewrite the equation as:
∠P+12∠ABC+∠BCP=180∘(1)
Similarly, in triangle QAD, we can also apply the angle sum property:
∠AQR+∠QAD+∠DAQ=180∘
Let ∠AQR=∠Q and ∠QAD=12∠ADC (since DQ is the bisector of ∠ADC). Thus, we can rewrite this equation as:
∠Q+12∠ADC+∠DAQ=180∘(2)
Now, we will add equations (1) and (2):
(∠P+12∠ABC+∠BCP)+(∠Q+12∠ADC+∠DAQ)=180∘+180∘
This simplifies to:
∠P+∠Q+12∠ABC+12∠ADC+∠BCP+∠DAQ=360∘
Since ABCD is a quadrilateral, the sum of its angles is 360∘:
∠A+∠B+∠C+∠D=360∘
Thus, we can equate:
∠BCP+∠DAQ=∠A+∠C
Substituting ∠BCP+∠DAQ into our previous equation, we get:
∠P+∠Q+12∠ABC+12∠ADC+∠A+∠C=360∘
Now, since ∠A+∠C=360∘−(∠ABC+∠ADC):
∠P+∠Q+12∠ABC+12∠ADC+(360∘−(∠ABC+∠ADC))=360∘
This simplifies to:
∠P+∠Q+12∠ABC+12∠ADC=180∘
Rearranging gives us:
∠P+∠Q=12(∠ABC+∠ADC)
Thus, we have proved that:
∠P+∠Q=12(∠ABC+∠ADC)
Topper's Solved these Questions
Similar Questions
In Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at Pand Q respectively. Prove that : ∠P+∠Q=12(∠ABC+∠ADC)
View SolutionIn Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
View SolutionIn the figure bisector of ∠B & ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
View SolutionIn the figure bisector of ∠B & ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that
∠P+∠Q=12(∠ABC+∠ADC).
View SolutionIn triangle ABC, AD and aEarn ABCD is a rhombus, AB is produced In the figure bisector of B and D of quadrilateral ABCD meet CO and AB produced and Q respectively. Prove that angle P t angle Q (angle ABC t le ADC). A
View SolutionIn a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B)
View SolutionIn a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B).
View SolutionIn a quadrilateral ABCD,AO andBO are the bisectors of ∠A and ∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionIn quadrilateral ABCD, AO and BO are the bisectors of ∠A and ∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View Solution
