Prove that In a parallelogram, opposite sides are equal.
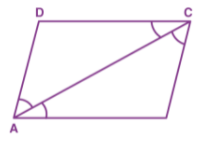
In parallelogram ABCD,
Consider,
AD∣∣BC and AB is transversal
∠A+∠B=180 [Co – int. Angles]
Now, consider AB∣∣DC and BC transversal
∠B+∠C=180 [Co – int. Angles]
From above equations we get
∠A+∠B=∠B+∠C
∠A=∠C
Similarly,
∠B=∠D
Topper's Solved these Questions
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.3
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.4
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.1
Explore 1 Video
- LINES AND ANGLESBook:NCERTChapter:LINES AND ANGLESExercise:SOLVED EXAMPLES
Explore 8 Videos
- NUMBER SYSTEMSBook:NCERTChapter:NUMBER SYSTEMSExercise:EXERCISE 1.4
Explore 2 Videos
Similar Questions
Knowledge Check
Is quadrilateral ABCD a parallelogram?
I. Its opposite sides are equal.
II. Its opposite angles are equal.
The correct answer is : (a) /(b)/(c )/(d).Aif the question can be answered by one of the given statements alone and not by the other,Bif the quesiton can be answered by either statement alone,Cif the question can be answered by both the statements together but not by any one of the two,Dif the question cannot be answered by using both the statements together.
Prove that in a parallelogram, opposite angles are equal.
View SolutionA quadrilateral is a parallelogram if its opposite sides are equal.
View SolutionAssertion: Every rectangle is a parallelogram.
Reason: Rectangle satisfies all the properties of parallelogram as opposite sides are equal and parallel, diagonals biseect each other and opposite angles are equal.
View SolutionProve that of all parallelograms of which the sides are given, the parallelogram which is rectangle has the greatest area.
View SolutionA quadrilateral is parallelogram if its opposite sides are equal
View SolutionUsing dot product of vectors; prove that a parallelogram; whose diagonal are equal; is a rectangle.
View SolutionUsing dot product of vectors, prove that a parallelogram, whose diagonals are equal, is a rectangle
View Solution

