Prove that a diagonal of a parallelogram divides it into two congruent triangles.
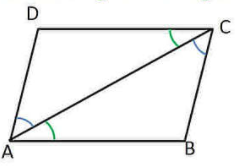
opposites sides of parallelogram are parallel. Thus
So, AB∣∣DC and AD∣∣BC.
In △ABC and △ADC,
∠BAC=∠DCA
AC=AC (common)
∠DAC=∠BCA
Thus, with ASA congruency, △ABC and △ADC are congruent.
Topper's Solved these Questions
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.2
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.3
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 7.8
Explore 1 Video
- LINES AND ANGLESBook:NCERTChapter:LINES AND ANGLESExercise:SOLVED EXAMPLES
Explore 8 Videos
- NUMBER SYSTEMSBook:NCERTChapter:NUMBER SYSTEMSExercise:EXERCISE 1.4
Explore 2 Videos
Similar Questions
Knowledge Check
Prove that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order.
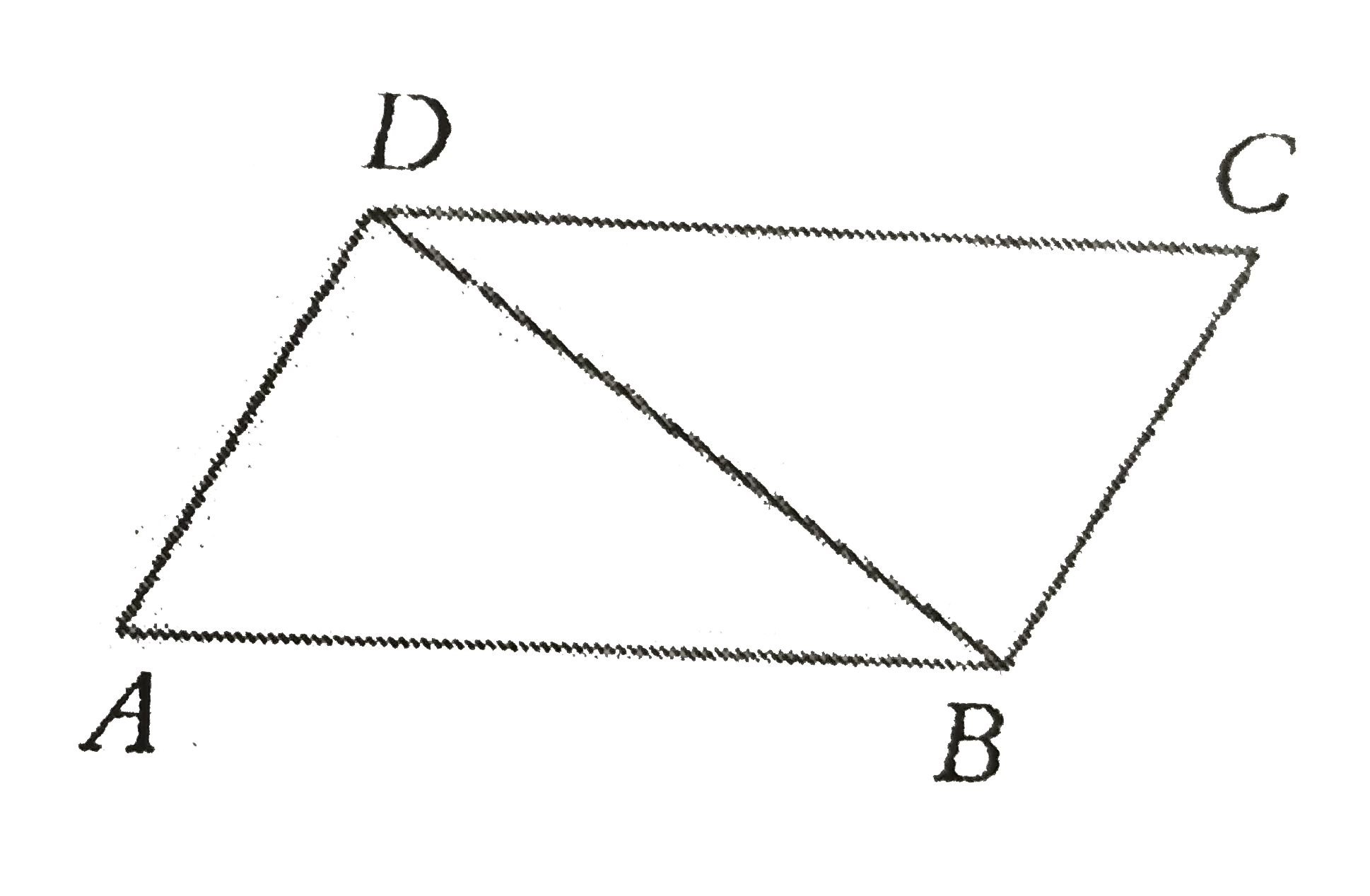
(A) By SSS conguruence property , ΔDAB≅ΔBCD.
(B) Let ABCD be a parallelogram and join BD.
(C ) AB=CD,AD=BC(opposite sides of parallelogram) and BD=BD (common side).
(D ) Similarly , AC divides the parallelogram into two congruent triangles.AABCDBBCADCBACDDCBAD
Prove that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order.

(A) By SSS conguruence property , ΔDAB≅ΔBCD.
(B) Let ABCD be a parallelogram and join BD.
(C ) AB=CD,AD=BC(opposite sides of parallelogram) and BD=BD (common side).
(D ) Similarly , AC divides the parallelogram into two congruent triangles.
View SolutionA diagonal of a parallelogram divides it into two triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area. GIVEN : A parallelogram ABCD . The diagonals AC and BD intersect at O. TO PROVE : ar(OAB)=ar(OBC)=ar(OCD)=ar(AOD)
View SolutionA diagonal of a parallelogram divides it into two triangles of equal area. GIVEN : A parallelogram ABCD in which BD is one of the diagonals. TO PROVE : ar (ABD)=ar(CDB)
View Solution

