Prove that in a parallelogram, opposite angles are equal.
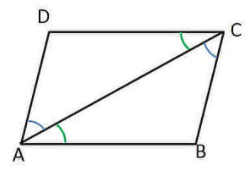
Since AB∣∣DC and AC is transversal,
∠BAC=∠DCA
Since AD∣∣BC and AC is transversal,
∠DAC=∠BCA
Adding the equations,
∠DAC+∠BAC=∠DCA+∠BCA
∠BAD=∠DCB
Similarly, we can prove,
∠ADC=∠ABC
Topper's Solved these Questions
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.5
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.6
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.3
Explore 1 Video
- LINES AND ANGLESBook:NCERTChapter:LINES AND ANGLESExercise:SOLVED EXAMPLES
Explore 8 Videos
- NUMBER SYSTEMSBook:NCERTChapter:NUMBER SYSTEMSExercise:EXERCISE 1.4
Explore 2 Videos
Similar Questions
In a parallelogram opposite sides are equal
View SolutionProve that In a parallelogram, opposite side are equal
View SolutionProve that in a parallelogram, opposite angles are equal.
View SolutionThe converse of the above properties are also true i.e.(i) A quadrilateral is a parallelogram if its opposite sides are equal.(ii)A quadrilateral is a parallelogram if its opposite angles are equal.(iii) A quadrilateral is a parallelogram if it has one pair of opposite sides parallel and equal.(iv) A quadrilateral is a parallelogram if its diagonals bisect each other .
View SolutionProve that In a parallelogram, opposite sides are equal.
View SolutionA quadrilateral is parallelogram if its opposite angles are equal.
View SolutionUsing dot product of vectors; prove that a parallelogram; whose diagonal are equal; is a rectangle.
View SolutionUsing dot product of vectors, prove that a parallelogram, whose diagonals are equal, is a rectangle
View SolutionA quadrilateral is a parallelogram if its opposite sides are equal.
View SolutionUsing dot product of vectors; prove that a parallelogram; whose diagonal are equal; is a rectangle.
View Solution

