In ΔABC the lines are drawn parallel to BC,CA and AB respectively through A,B and C intersecting at P, Q and R. Find the ration of perimeter of ΔPQR and ΔABC
Clearly, ABCQ and ARBC are parallelograms.
∴BC=AQ and BC=AR
⇒AQ=AR
⇒A is the mid-point of QR.
Similarly, B and C are the mid-points of PR and PQ respectively.
∴AB=12PQ
BC=12QR
CA=12PR
⇒PQ=2AB
QR=2BC
PR=2CA
⇒PQ+QR+RP=2(AB+BC+CA)
⇒Perimeter of △PQR=2(Perimeter of △ABC)
Hence, the ratio is 1:2.
Topper's Solved these Questions
Similar Questions
In ΔABC the lines are drawn parallel to BC,CA and AB respectively through A,B and C intersecting at P, Q and R. Find the ration of perimeter of ΔPQR and ΔABC
View SolutionABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P, Q and R . Prove that the perimeter of PQR is double the perimeter of ABC
View Solution
Knowledge Check
In ΔABC, the line parallel to BC Intersects AB and AC at P and Q respectively. If AB:AP=5:3then AQ:QCis :
A3:2B2:3C3:5D1:2Let →a,→b,→c form sides BC,CA and AB respectively of a triangle ABC then
Aa.b+b.c+c.a=0Ba×b=b×c=c×aCa.b=b.c=c.aDa×b+b×c+c×a=0AL, BM and CN are perpendicular from angular points of a triangle ABC on the opposite sides BC, CA and AB respectively. Δ is the area of triangle ABC, (r ) and R are the inradius and circumradius.
If perimeters of ΔLMNandΔABCanλandμ, then the value of λμ isArRBRrCrRΔDΔrR
Triangle ABC is formed by the lines 7x−y+3=0,x+y−3=0andx−3y−31=0, Three new lines are drawn parallel to BC,CA,AB passing through A,BandC intersecting each other at P, Q and R respectively the circum centre of ΔPQR lies on
View SolutionIn ΔABC, PQ is parallel to BC, while P and Q are at AB and AC respectively. If AB = 3AP, then what is the ratio of areas of triangles ΔAPQ and ΔABC.
View SolutionLet →a,→b,→c form sides BC,CA and AB respectively of a triangle ABC then
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through AandC, lines are drawn parallel to BCandPA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
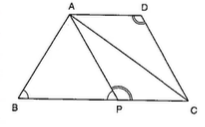
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through A and C, lines are drawn parallel to BC and PA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
View Solution
