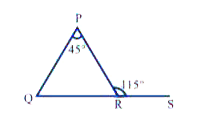In Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

Video Solution
Text Solution
In∠PQR
∠PRS=∠PQR+∠QPR(exterior angle of triangle)
12∠PRS=12∠PQR+12∠QPR
∠TRS=∠TQS+12∠QPR−(1)
In∠QTS
∠TRS=∠TQR+∠QTR−(2)
∠TQS+∠QTR=∠TQS+12∠QPR
∠QTR=12∠QPR
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.16videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE 6.26videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - EXERCISE 4.42videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.121videos
NCERT THEOREMS
Similar Questions
Knowledge Check
- Question 1 - Select One
P is the father of Q and R is the son of S. T is the brother of P. Q is the sister of R. How is S related to T?
Aa) BrotherBb) DaughterCc) Sister-in-lawDd) Brother-in-law
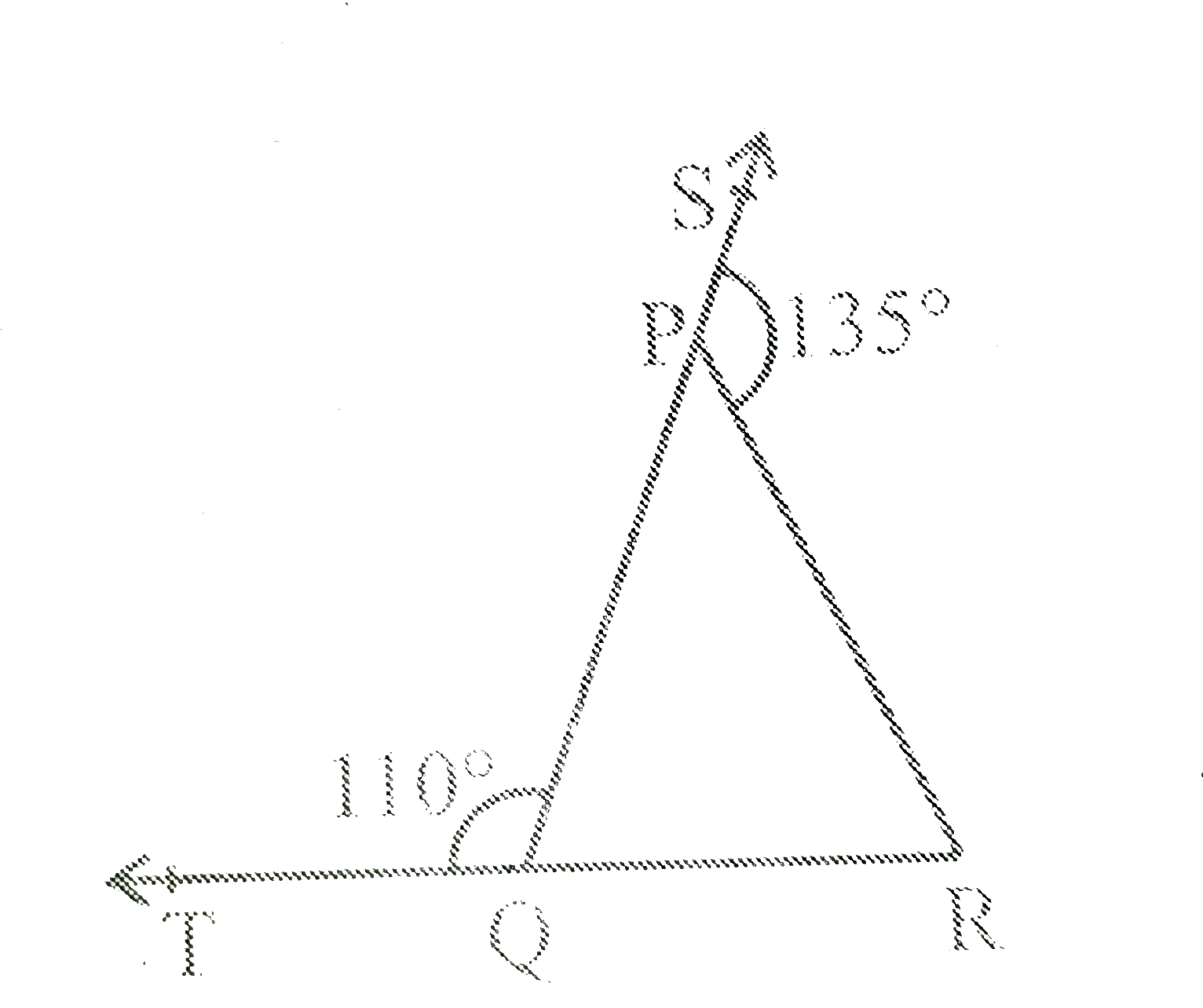
In Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
 View Solution
View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
 View Solution
View SolutionIn Fig. 4.90, if PSQR , prove that POS~ROQ . (FIGURE)
View SolutionIn Fig. 4.90, if POS~ROQ , prove that PSQR . (FIGURE)
View SolutionIn Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.
 View Solution
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
 View Solution
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
 View Solution
View Solution