In Fig. 6.24, if PQ∣∣RS,∠MXQ=135∘ and∠MYR=40∘, find∠XMY..

Draw a line AB parallel to PQ, so AB∥PQ and PQ∥RS, so AB∥RS.
It is known that the sum of two interior angles on the same side is 180∘
, therefore,
∠QXM+∠XMB=180∘
∠XMB=180∘−135∘∠XMB=45∘
It is also known that the alternate interior angles are equal, so,
∠BMY=∠MYR
∠BMY=40∘
Now,∠XMY=∠XMB+∠BMY=45∘+40∘=85∘
Topper's Solved these Questions
Similar Questions
In Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.

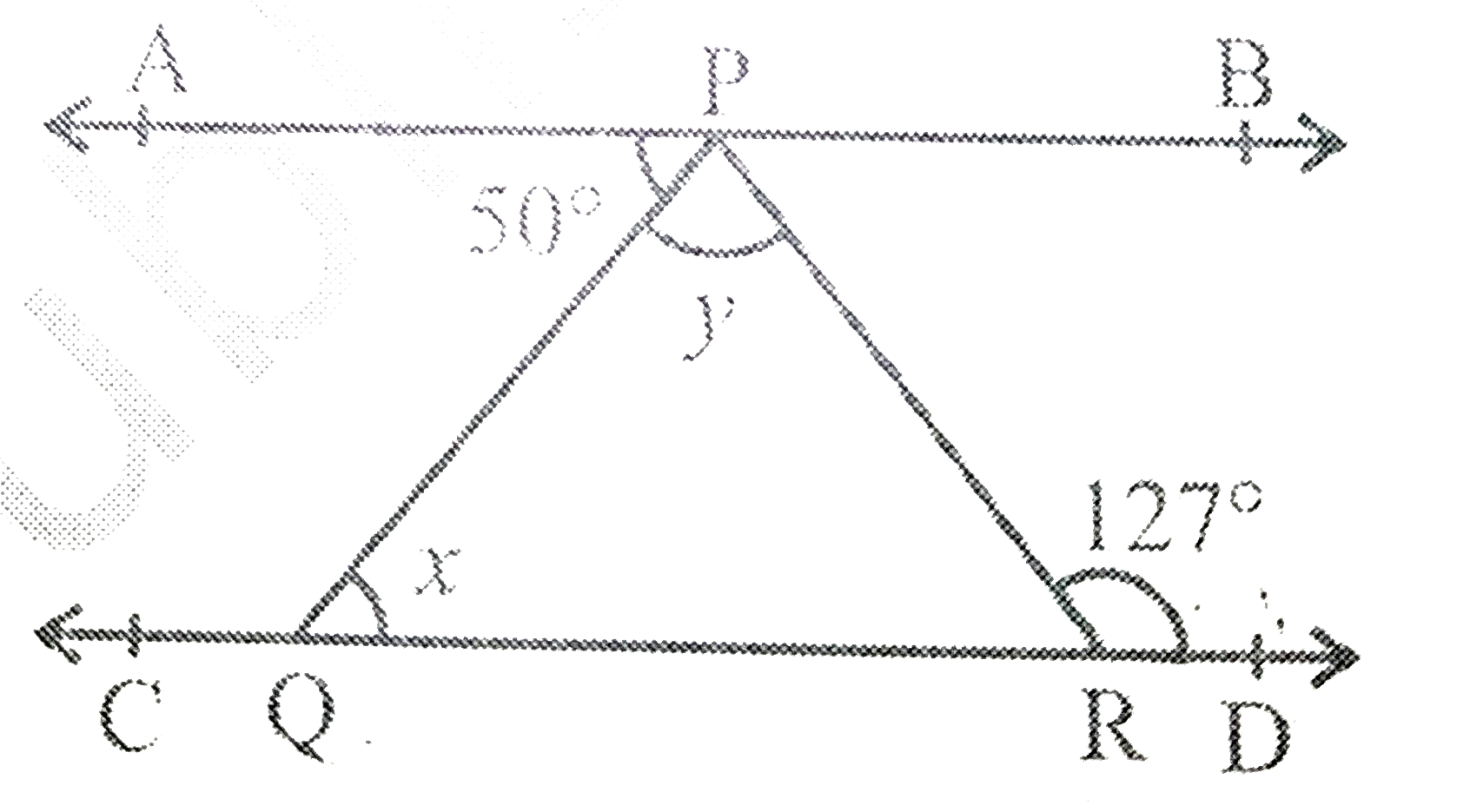
View SolutionIn Fig. 6.32, if AB∣∣CD,∠APQ=50∘and∠PRD=127∘, find x and y.
View SolutionIn Fig. 6.43, if PQ⊥PS,PQ∣∣SR,∠SQR=28∘ and ∠QRT=65∘, then find the values of x and y.

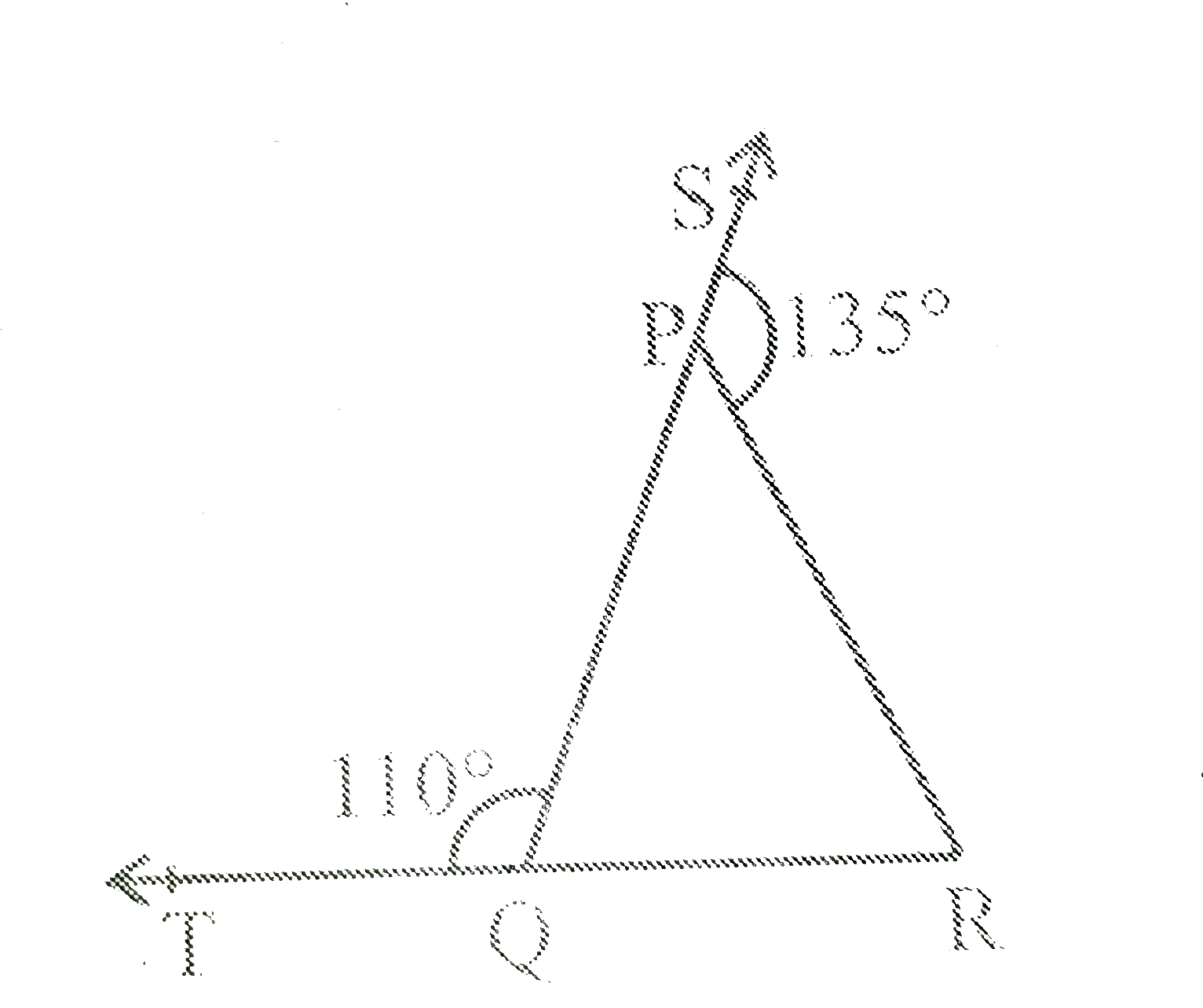
View SolutionIn Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.

View SolutionIn Fig. 4.230, each of PA, QB, RC and SD is perpendicular to l . If AB=6cm , BC=9cm , CD=12cm and PS=36cm , then determine PQ, QR and RS . (FIGURE)
View SolutionIn Fig. 4.245, RSDBPQ . If CP=PD=11cm and DR=RA=3cm . Then the values of x and y are respectively (FIGURE) 12, 10 (b) 14, 6 (c) 10, 7 (d) 16, 8
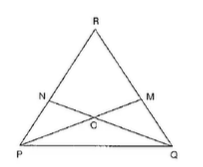
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
View SolutionIn Fig.88 PR is a straight line and ∠PQS:∠SQR=7:5. The measure of ∠SQR is (a) (b)(c)(d)(e)60(f)0(g)(h)(i) (j) (b) (k)(l)62(m)(n)(o)1p2(q)(r)(s)0(t)(u)(v) (w) (c) (d)(e)67(f)(g)(h)1i2(j)(k)(l)0(m)(n)(o) (p) (d) (q)(r)(s)(t)75(u)0(v)(w)(x) (y)
View SolutionIn Fig. 4.177, ACBAPQ . If BC=10cm, PQ=5cm, BA=6.5cm and AP=2.8cm find CA and AQ . Also, find the area (ACB):area (APQ) . (FIGURE)
View Solution
