Question

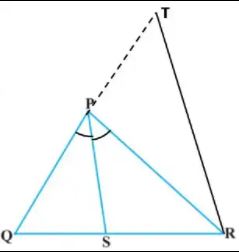
In figure PS is the bisector of $\angle QPR$of $\Delta PQR$. Prove that $\frac{QS}{SR}=\frac{PQ}{PR}$.

Explanation

In `△QRT`
`RT∣∣SP ` [By construction]
And PS intersects QT and QR at two distinct points P and Q.


Therefore,


QT and QR will be divided in the same ratio


`(QS)/(SR) = (PT)/(PQ)`......(1)


[Basic proportionality theorem: If a line is drawn parallel to one side of a triangle, intersecting the other two sides at distinct points, then the other two sides are divided in the same ratio.]


Now,
`RT∣∣SP`


and PR is the transversal


Therefore,



`∠SPR=∠PRT....(2) `


[Alternate interior angles]
and
`∠QPS=∠PTR`....(3)


[Corresponding angles]


Also, given the
PS is the bisector of `∠QPR
∠QPR=∠SPR`


From (2) and (3)


`∠PTR=∠PRT`


Therefore, `PT=PR` [Sides opposite to equal angles of a triangle are equal]


Putting `PT=PR` in (1)


`(QS)/(SR)= (PQ)/(PT)`
​


Hence proved.