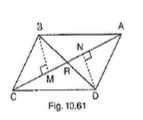
In fig., D is a point on hypotenuse AC of $Δ A B C, D M ⊥ B C$ and $D N ⊥ A B$ . Prove that
(i) $D M^{2} = D N \cdot M C$
(ii) $D N^{2} = D M \cdot A N$

Video Solution

Text Solution

Verified by Experts

1)BNDM is rectangle
BM=DN
DM=BN
In $∠ D M C and ∠ B M D$
$∠ C = ∠ D$
$∠ M = ∠ M$
$∠ D M C and ∠ B M D$ (AAA)
$\frac{D M}{B M} = \frac{M C}{M D}$
DMMD=MCDN
DM^2=MCDN.
Similarly, DN^2=DMAN.

Updated on:21/07/2023

|

Class 10 MATHS TRIANGLES

Similar Questions

In Figure, $B M a n d D N$ are both perpendiculars to the segments $A C a n d B M = D N$ . Prove that $A C$ bisects $B D$

View Solution
ABC is a triangle right-angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) $M D ⊥ A C$
(iii) $C M = M A = \frac{1}{2} A B$
View Solution
In right triangle $A B C$ , right angle at $C, M$ is the mid-point of the hypotenuse $A B .$ $C$ is jointed to $M$ and produced to a point $D$ such that $D M = C M .$ Point $D$ is joined to point $B .$ Show that $A M C ≅ B M D$ (ii) $∠ D B C = 90^{\circ}$ (iii) $D B C ≅ A C B$ (iv) $C M = \frac{1}{2} A B$
View Solution
In right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that $D M = C M$ . Point D is joined to point B (see Fig. 7.23). Show that:
(i) $Δ A M C ≅ Δ B M D$
(ii) $∠ D B C$ is a right angle
(iii) $Δ D B C ≅ Δ A C B$
(iv) $C M = \frac{1}{2} A B$

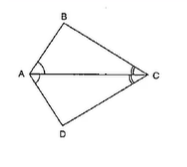
View Solution
In Figure, diagonal $A C$ of a quadrilateral $A B C D$ bisects the angles $A a n d C$ . Prove that $A B = A D a n d C B = C D$

View Solution
ABCD is a quadrilateral in which and $∠ D A B = ∠ C B A$ (see Fig. 7.17). Prove that
(i) $Δ A B D ≅ Δ B A C$
(ii) $B D = A C$
(iii) $∠ A B D = ∠ B A C$

View Solution
In a $A B C$ , If $L and M$ are points $A B and A C$ respectively such that $L M parallel B C$
Prove that: $a r (A B M) = a r (A C L)$
View Solution
$A B C a n d D B C$ are two isosceles triangles on the same bas $B C$ and vertices $A a n d D$ are on the same side of $B C$ . If $A D$ is extended to intersect $B C$ at $P,$ show that $A B D ≅ A C D$ (ii) $A B P ≅ A C P$
View Solution
$A B C D$ is a parallelogram. $L a n d M$ are points on $A B a n d D C$ respectively and $A L = C M$ . Prove that $L M a n d B D$ bisect each other.
View Solution
In a $A B C,$ If $L and M$ are points on $A B and A C$ respectively such that $L M parallel B C$
Prove that: $a r (L B C) = a r (M B C)$
View Solution

Recommended Questions

Home
Ask Doubt
Profile