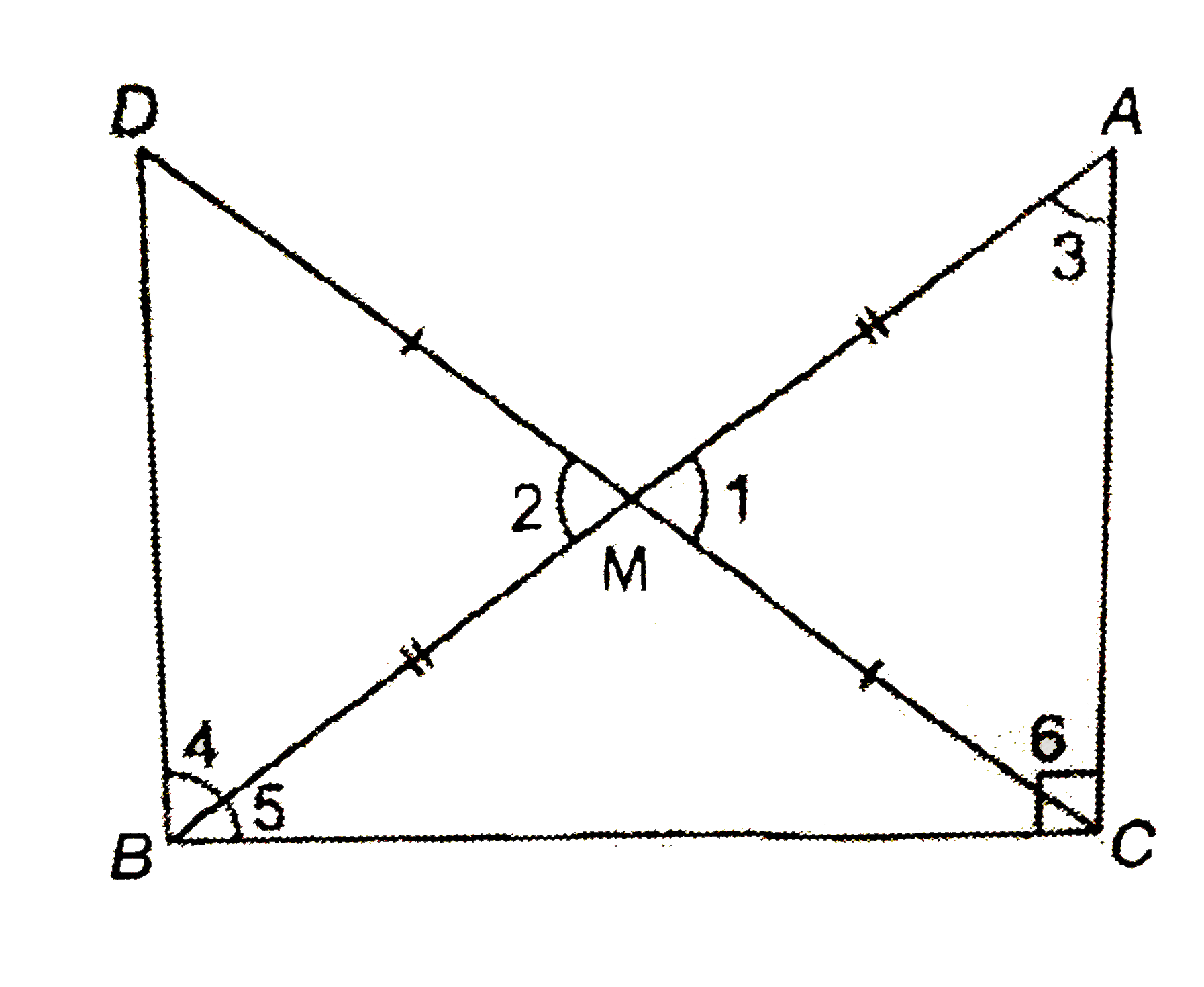
In right triangle $A B C$ , right angle at $C, M$ is the mid-point of the hypotenuse $A B .$ $C$ is jointed to $M$ and produced to a point $D$ such that $D M = C M .$ Point $D$ is joined to point $B .$ Show that $A M C ≅ B M D$ (ii) $∠ D B C = 90^{\circ}$ (iii) $D B C ≅ A C B$ (iv) $C M = \frac{1}{2} A B$

Video Solution

Text Solution

Verified by Experts

Given: $M$ is the mid-point of hypotenuse $A B$ , $∠ C = 90 °$ and $D M = C M$
To Prove:
(i) $△ A M C ≅ △ B M D$
(ii) $∠ D B C$ is a right angle.
(iii) $△ D B C ≅ △ A C B$
(iv) $C M = \frac{1}{2} A B$
Proof:
(i) In $△ A M C$ and $△ B M D$ ,
$A M = B M$ ( $M$ is the mid - point of $A B$ )
$∠ A M C = ∠ B M D$ (Vertically opposite angles)
$C M = D M$ (Given)
$∴ △ A M C ≅ △ B M D$ (By SAS congruence rule)
$∴ A C = B D$ (By CPCT)
Also, $∠ A C M = ∠ B D M$ (By CPCT)
(ii) $∠ D B C$ is a right angle.
$∠ A C M = ∠ B D M$ (proved above)
But, $∠ A C M$ and $∠ B D M$ are alternate interior angles. Since alternate angles are equal, it can be said that $D B ∣ ∣ A C$ .
$∠ D B C + ∠ A C B = 180 °$ (Co-interior angles)
$∠ D B C + 90 ° = 180 °$ [Since, $△ A C B$ is a right angled triangle]
$∴ △ D B C = 90 °$
Thus, $∠ D B C$ is a right angle.
(iii) In $△ D B C$ and $△ A C B$ ,
$D B = A C$ (proved above)
$∠ D B C = ∠ A C B = 90 °$ (Proved above)
$B C = C B$ (Common)
$∴ △ D B ≅ △ A C B$ (By $S A S$ congruence rule)
(iv) $C M = \frac{1}{2} A B$
Since $△ D B C ≅ △ A C B$
$A B = D C$ (By CPCT)
$\Rightarrow \frac{1}{2} A B = \frac{1}{2} D C$

$C M = \frac{1}{2} D C = \frac{1}{2} A B$
$∴ C M = \frac{1}{2} A B$
Hence proved.

Updated on:21/07/2023