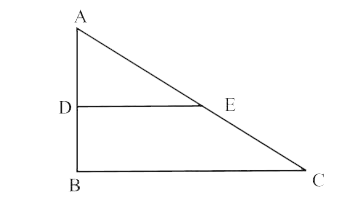
In Figure, triangle ABC
is right-angled at B.
Give that AB=9CM, AC=15CM,andD,E are the mid-points of the sides ABandAC respectively, calculate
The length of BC
(ii) The area of ADE
in traingle ABC,
∠B=900
so from pythagorus theorem, BC2=AC2−AB2
=152−92
BC=12cm
here D ,E are mid points of AB and AC
soDE∣∣BC
so ∠ADE=∠B=900
since DE is line joining mid points of AB ,AC so
DE=BC2=6cm
so area of
△ADE=(12)×9×6=27cm2
Topper's Solved these Questions
Similar Questions
In Figure, triangle ABC is right-angled at B. Give that AB=9CM, AC=15CM,andD,E are the mid-points of the sides ABandAC respectively, calculate
The length of BC
(ii) The area of ADE
View SolutionIn the figure, ΔABC is right angled at B. If AB = 9 cm, AC = 15 cm. and D and E are the mid points of AB & AC respectively calculate.
(i) The length of BC
(ii) The area of trapezium BCED
View Solution
Knowledge Check
If in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to
Aa4−b4Ba2−b2Cb4−a4Db2−a2ABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
A4:1B5:1C3:1Dcan't be determined
In the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View SolutionD, E, F are the mid-points of the sides BC, CA and AB respectively of a ABC . Determine the ratio of the areas of DEF and ABC .
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :

View SolutionIf D(3,-2) , E(-3,1) and F(4,-3) are the mid-points of the sides BC, CA and AB respectively of ΔABC , find the co-ordinates of point A , B and C .
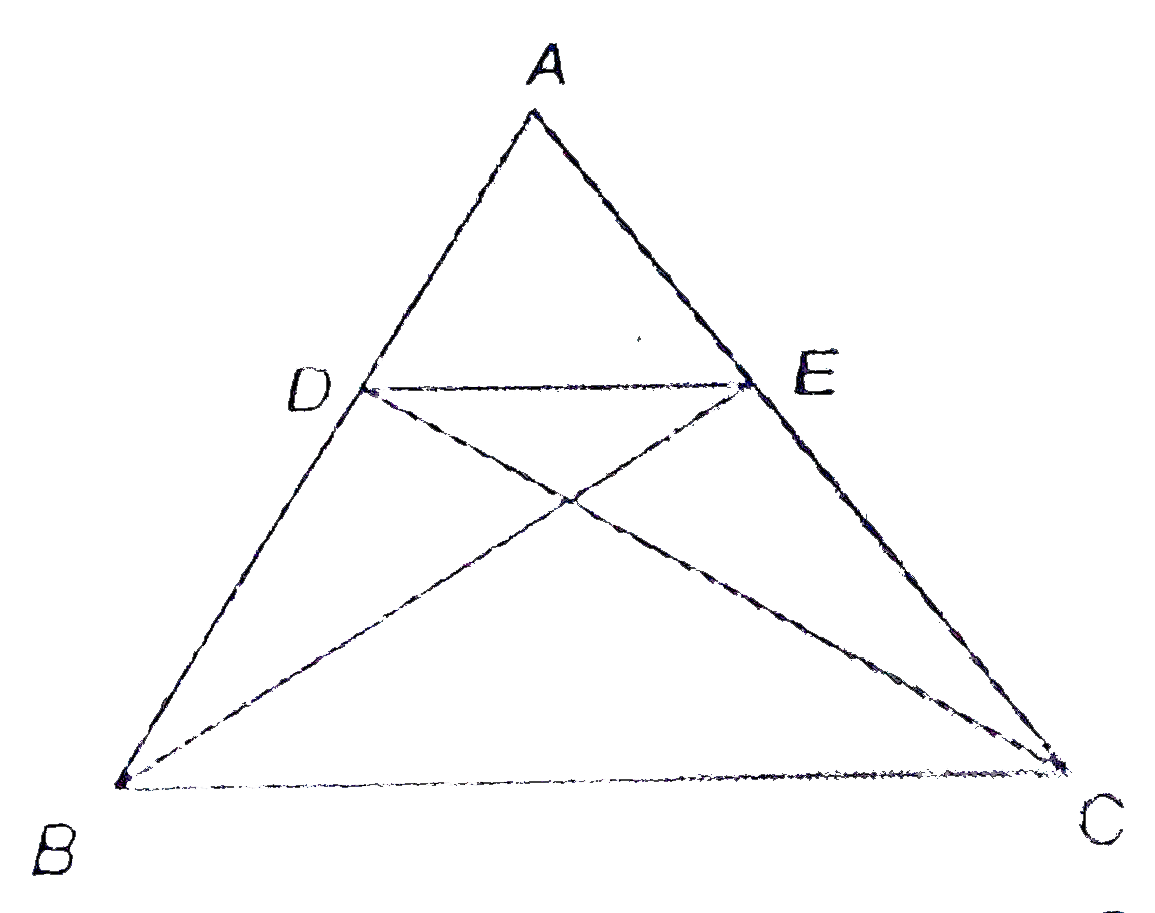
View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DEBC.
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC
View Solution
