In Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

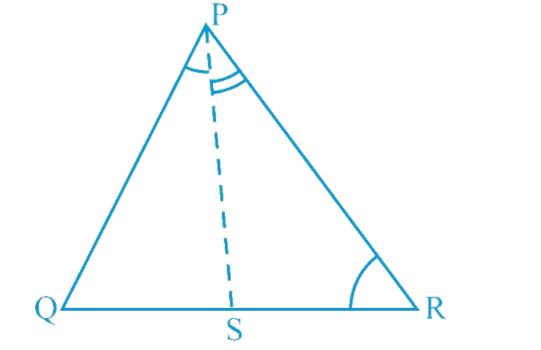
Given: PR>PQand PS bisects ∠QPR
To prove: ∠PSR>∠PSQ
As PR>PQ, ∠PQS>∠PRS (Angle opposite to larger side is larger ) ...(1)
PS is the angle bisector of ∠QPR.
∠QPS=∠RPS...(2) [Since,PS bisects ∠QPR]
∠PSR is the exterior angle of ΔPQS.
∠PSR=∠PQS+∠QPS ...(3) [Using exterior angle sum property]
∠PSQ is the exterior angle of ΔPRS.
∠PSQ=∠PRS+∠RPS...(4) [Using exterior angle sum property]
From Equations (1) and (2), we obtain
∠PQS+∠QPS>∠PRS+∠RPS
∠PSR>∠PSQ [From Equations (3) and (4)]
Topper's Solved these Questions
- TRIANGLESBook:NCERTChapter:TRIANGLESExercise:EXERCISE 7.1
Explore 8 Videos
- TRIANGLESBook:NCERTChapter:TRIANGLESExercise:EXERCISE 7.5
Explore 4 Videos
- TRIANGLESBook:NCERTChapter:TRIANGLESExercise:Solved Examples
Explore 9 Videos
- SURFACE AREAS AND VOLUMESBook:NCERTChapter:SURFACE AREAS AND VOLUMESExercise:EXERCISE 13.8
Explore 10 Videos
Similar Questions
In the given Fig. , if QTPR=QRQS and ∠1=∠2 . Prove that PQS~TQR . (FIGURE)
View SolutionIf P + Q = R and P - Q = S, prove that R2+S2=2(P2+Q2)
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.

View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.

View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
View SolutionIn Fig. 4.90, if PSQR , prove that POS~ROQ . (FIGURE)
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.

View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

View SolutionIn Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.

View SolutionIf PQRS is a square, then write the measure of ∠SRP
View Solution