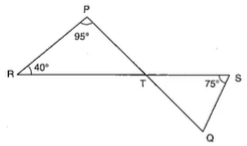
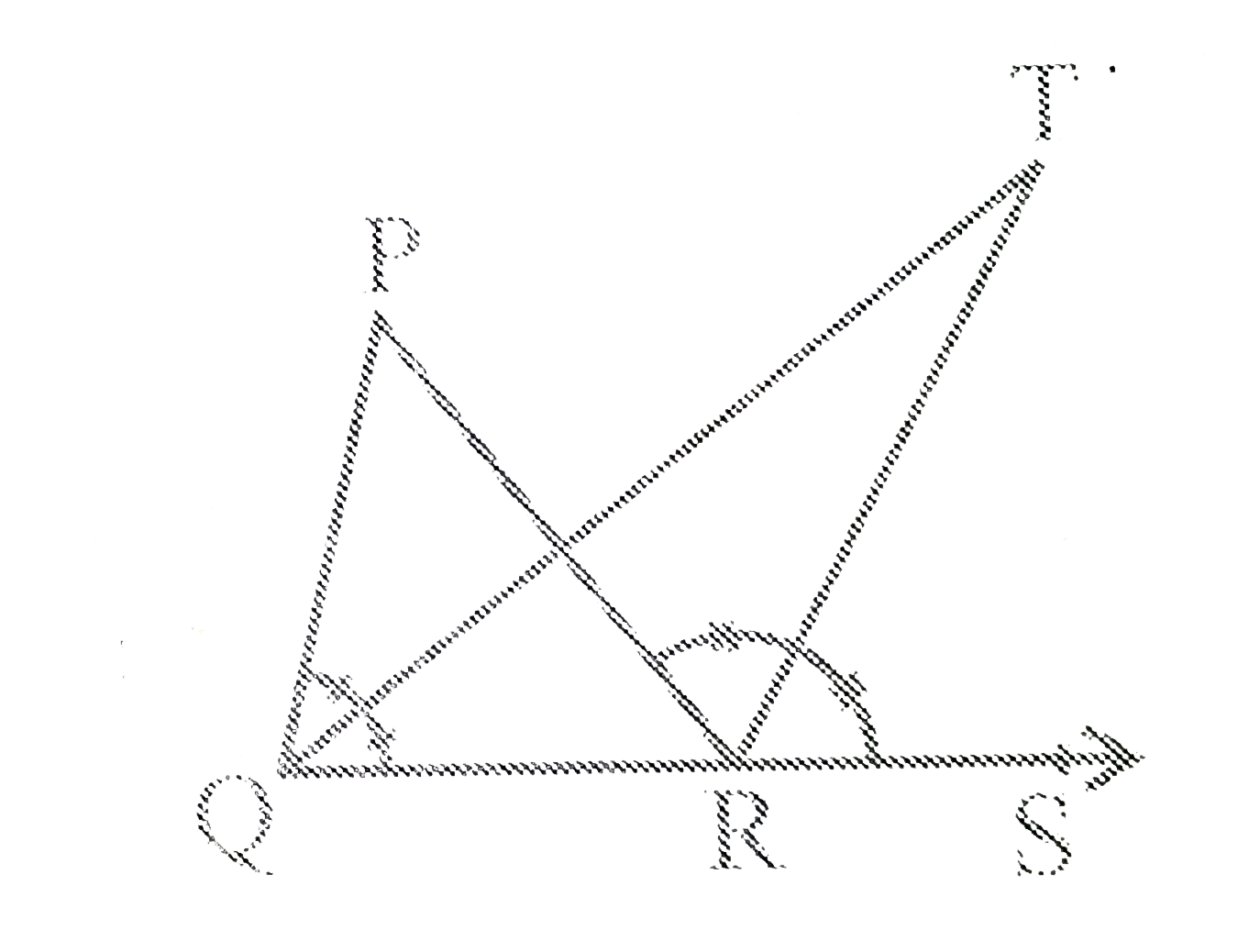
In Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.

∠PRT
∠PRT+∠RPT+∠PTR=1800
40o+95o+∠PTR=180o
∠PTR=450
∠QTS=∠PTR
∠QTS=45o
∠SQT
∠SQT+∠QTS+∠TSQ=180o
∠SQT+450+750=180o
∠SQT=60o
Topper's Solved these Questions
- LINES AND ANGLESBOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.1
6 Videos
- LINES AND ANGLESBOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE 6.2
6 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NCERTCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - EXERCISE 4.4
2 Videos
- NCERT THEOREMSBOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.12
1 Videos
Similar Questions
In Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.

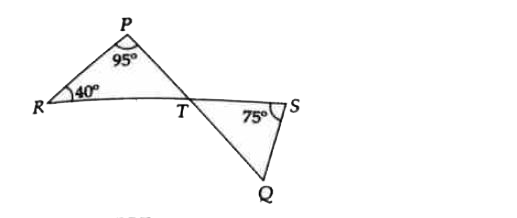
View SolutionIn figure, if lines PQ and RS intersect at a point T such that PRT=400,∠RPT=950 and ∠TSQ=750, find ∠SQT.
View SolutionIn the given figure lines PQ and RS intersect at point T such that ∠PRT=40∘∠RPT=95∘ and ∠TSQ=75∘ find ∠SQT
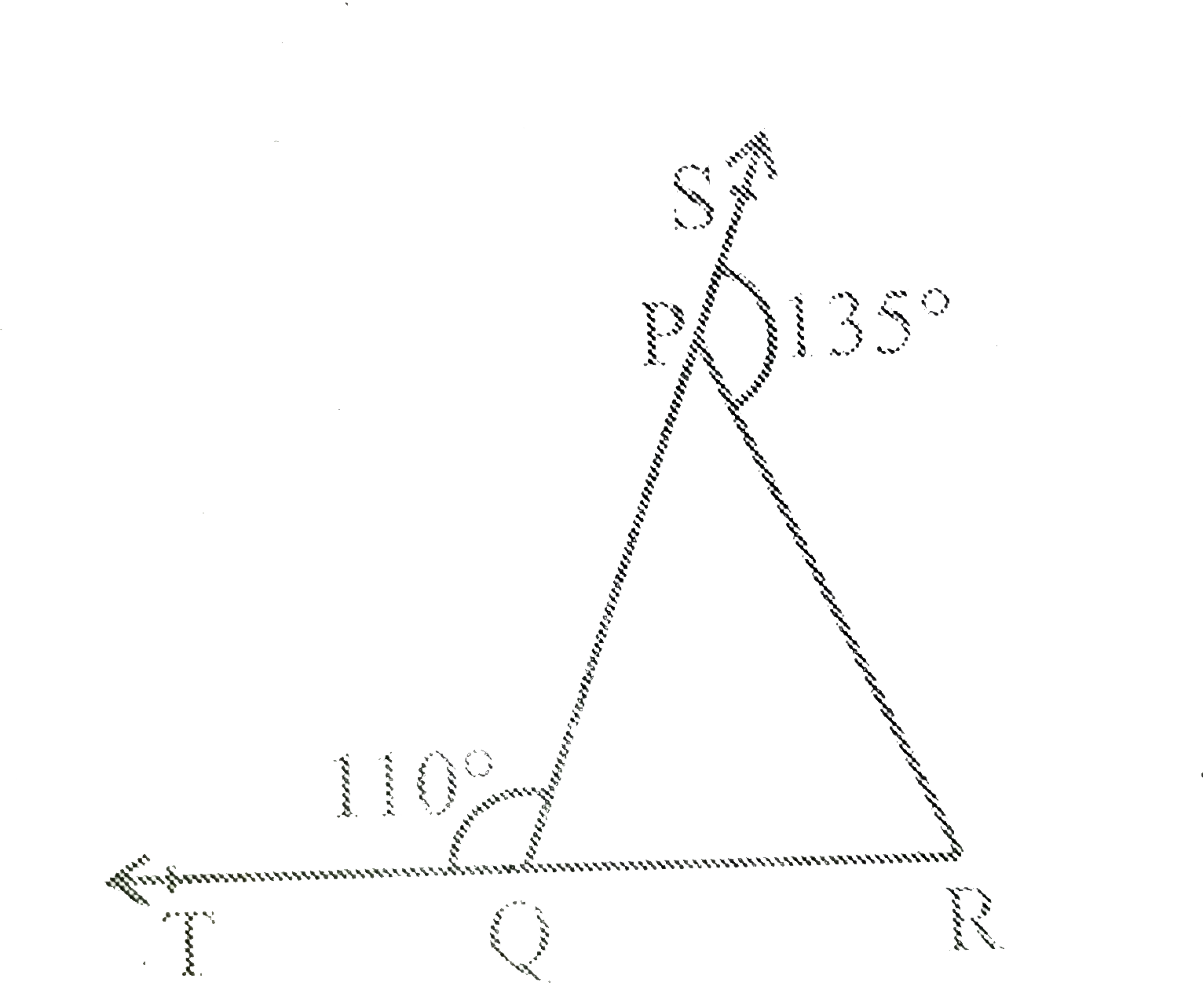
View SolutionIn Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
View SolutionIn Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.
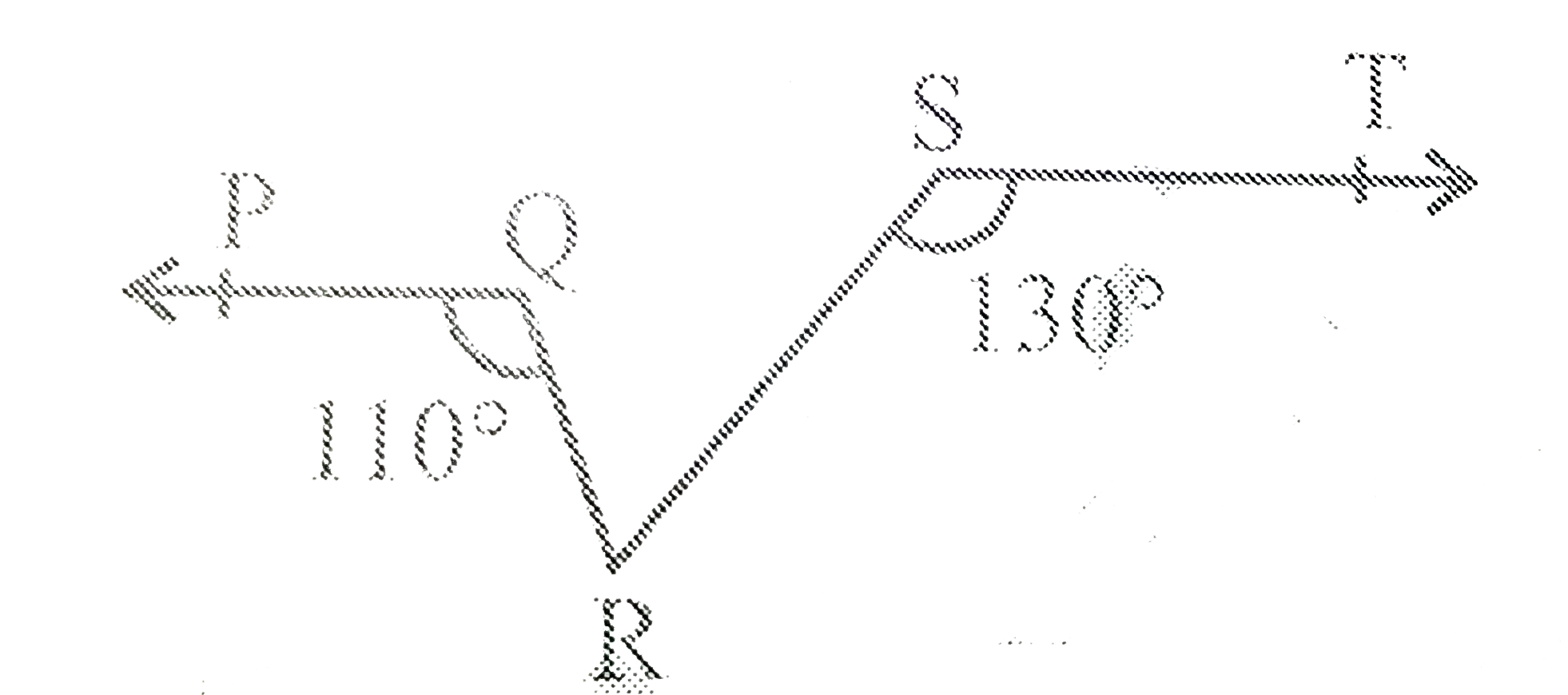
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.
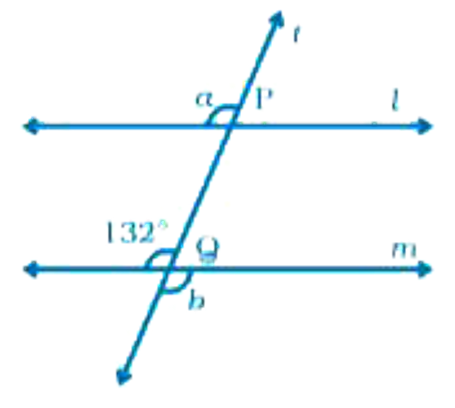
View SolutionIn Fig. 5.55, l ||m and a line t intersects these lines at P and Q, respectively. Find the sum 2a + b.
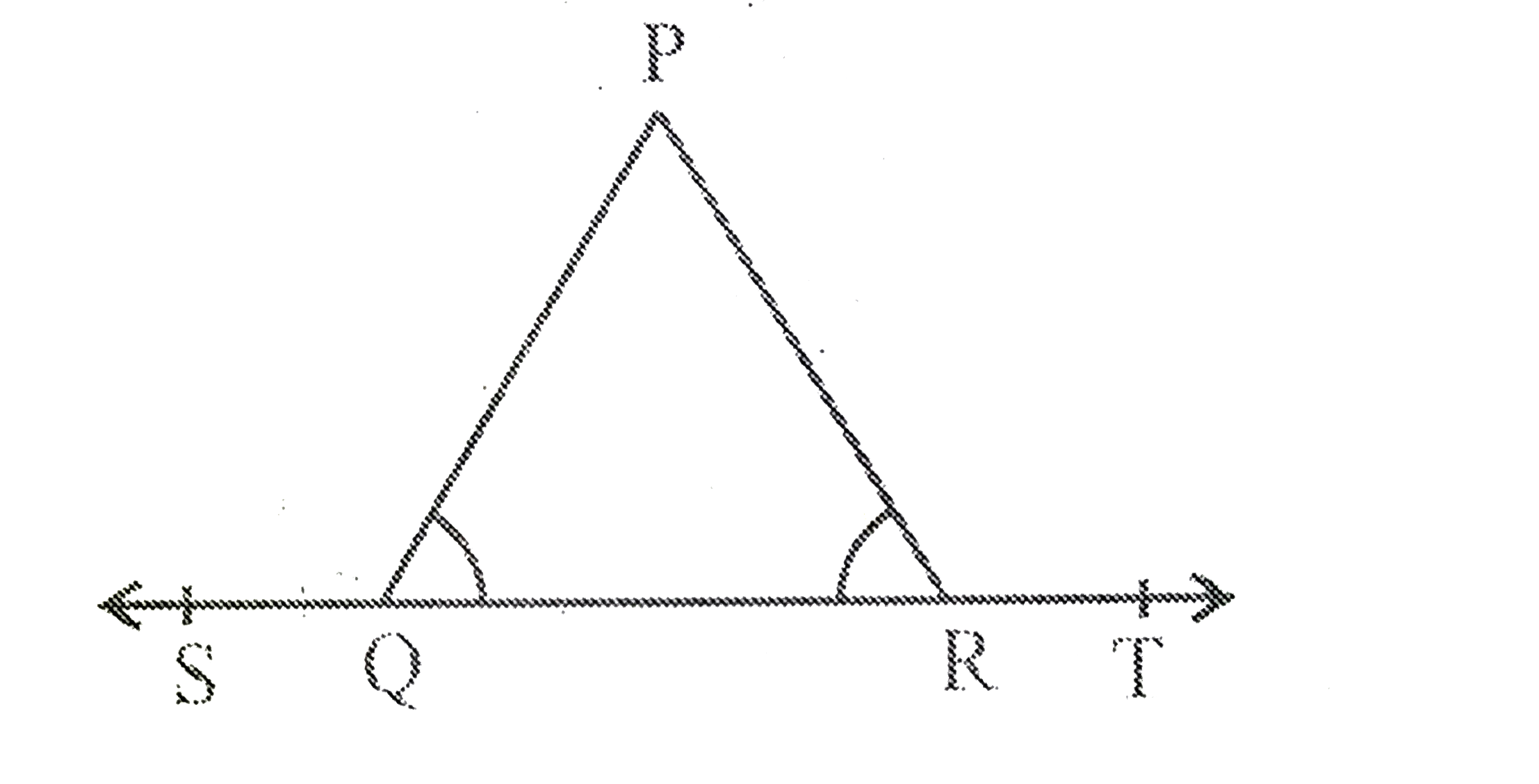
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
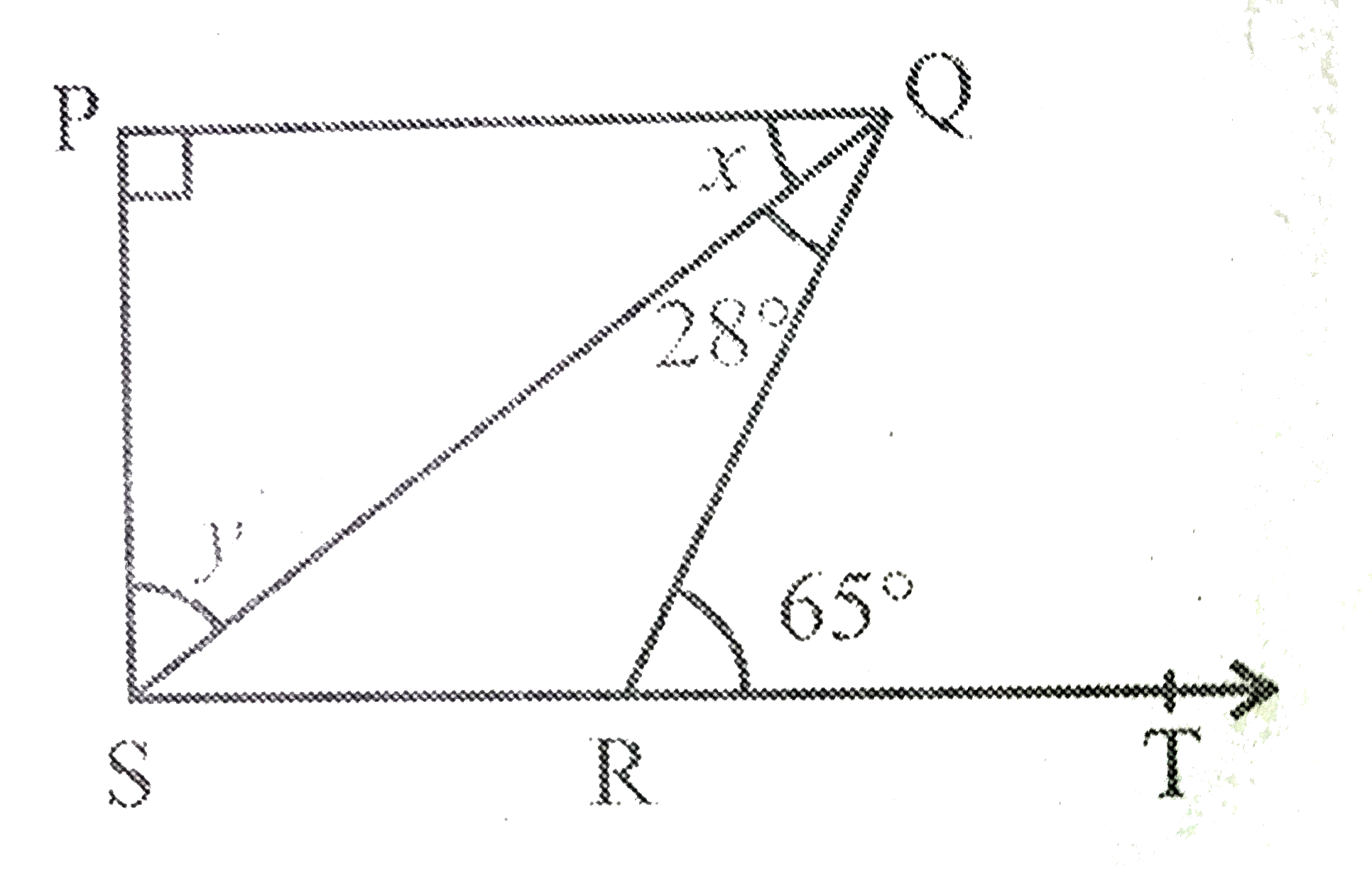
View SolutionIn Fig. 6.43, if PQ⊥PS,PQ∣∣SR,∠SQR=28∘ and ∠QRT=65∘, then find the values of x and y.
View Solution
