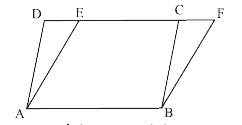
ABCD is a parallelogram and X is the mid-point of AB. (AXCD)=24cm2, then ar(ABC)=24cm2.
Video Solution
Text Solution
False
Given, ABCD is a parallelogram and ar(AXCD)=24cm2
Let area of parallelogram ABCD is 2ycm2 and join AC.

We know that, diagonal divides the area of parallelogram in two equal areas.
∴ ar(ΔABC)=ar(ACD)=y [say]
Also, X is the mid-point of AB.
So, ar(ΔACX)=ar(BCX) [since, X is median in ΔABC]
=12ar(ABC)=12y
Now, ar (AXCD)=ar(ΔADC)+ar(ACX)
24=y+y2 [given]
⇒ 243y2
⇒ y=24×23=16cm2
Hence, ar(ΔABC)=16cm2
Therefore, given statement is false.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by ACIn the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
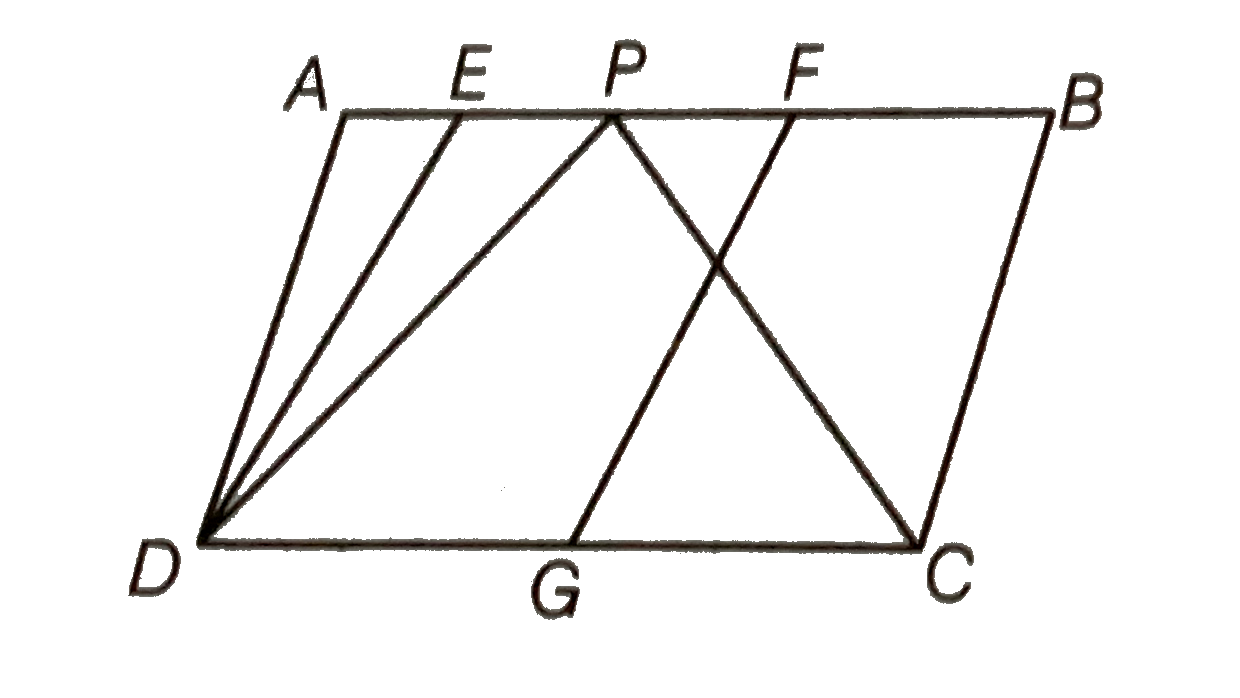 ATrueBFalseCPartially trueDNone of these
ATrueBFalseCPartially trueDNone of theseIn the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
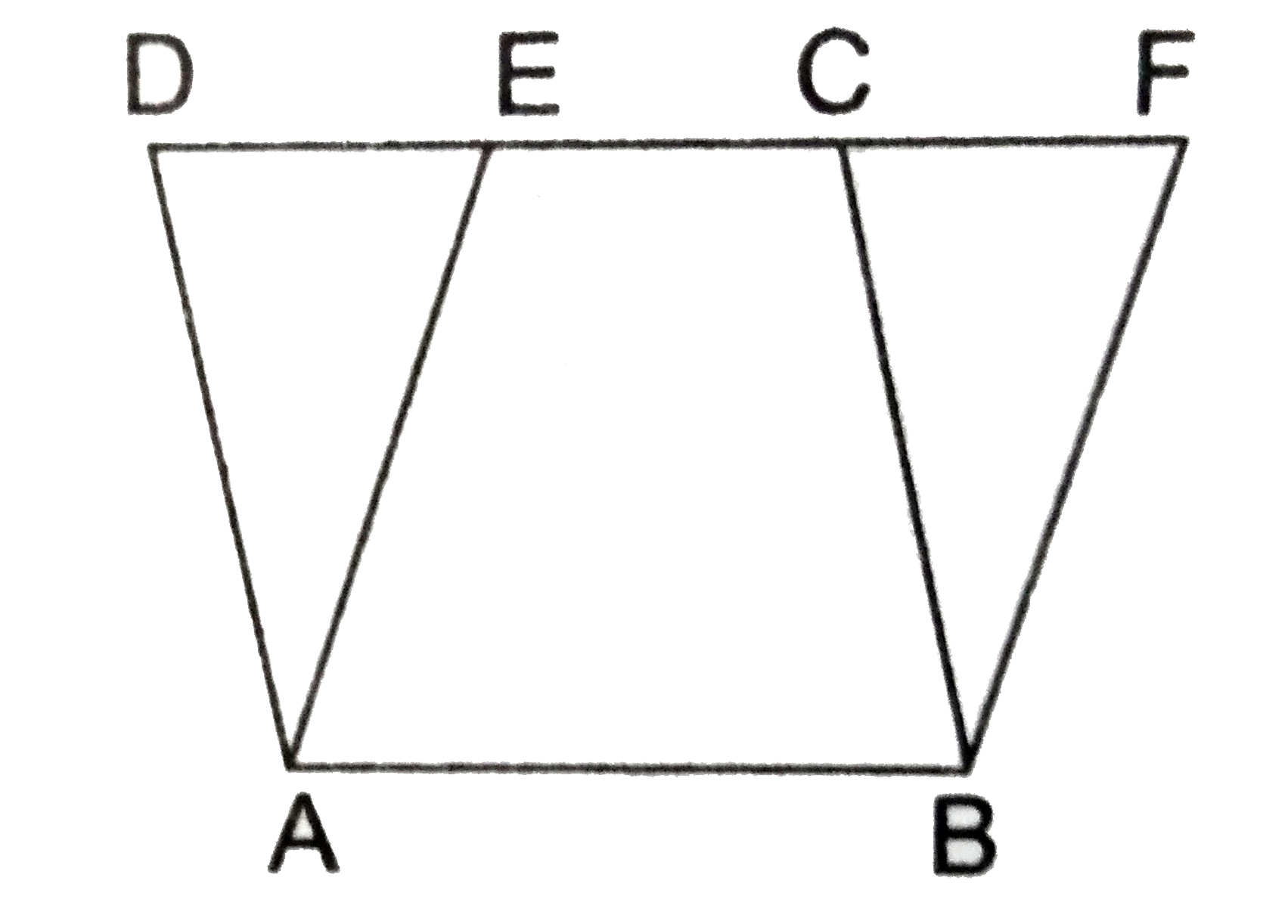 A4cm2B4.8cm2C6cm2D8cm2
A4cm2B4.8cm2C6cm2D8cm2
ABCD is a parallelogram and O is the point of intersection of its diagonals. If ar(△AOD)=4cm2 find ar(△AOB)
View SolutionABCD is a parallelogram, P is the mid point of AB. BD and CP intersects at Q such that CQ:QP=3:1. If ar(ΔPBQ)=10cm2, find the area of parallelogram ABCD.
View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
View SolutionIn the given figure, ABCD and ABFE are parallelograms such that ar(quad. EABC) =19 cm2 and ar(||gm ABCD) = 28 cm2. Then, ar(△BCF) is
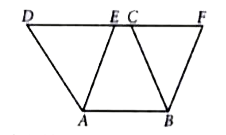
View SolutionABCD is a parallelogram P and R are two points on AB such that the area of parallelogram ABCD is 8 times the area of Δ DPR. If PR = 5 cm, then CD is equal to
View Solution