Question

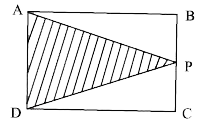
ABCD is a parallelogram P and R are two points on AB such that the area of parallelogram ABCD is 8 times the area of $\Delta$ DPR. If PR = 5 cm, then CD is equal to

Options

A. 10 cm
B. 5 cm
C. 20 cm
D. 12 cm

Answer

C

Explanation

To solve the problem step by step, we need to find the length of CD in the parallelogram ABCD given that the area of parallelogram ABCD is 8 times the area of triangle DPR and that PR = 5 cm.

1. Understand the Given Information:
- ABCD is a parallelogram.
- P and R are points on AB.
- Area of parallelogram ABCD = 8 × Area of triangle DPR.
- Length of PR = 5 cm.

2. Area of Parallelogram:
- The formula for the area of a parallelogram is:
\( \text{Area of parallelogram} = \text{Base} \times \text{Height} \)
- Let the base be AB and the height be h. Thus:
\( \text{Area of parallelogram ABCD} = AB \times h \)

3. Area of Triangle DPR:
- The formula for the area of a triangle is:
\( \text{Area of triangle} = \frac{1}{2} \times \text{Base} \times \text{Height} \)
- Here, the base is PR (which is 5 cm) and the height is also h (same height as the parallelogram). Thus:
\( \text{Area of triangle DPR} = \frac{1}{2} \times PR \times h = \frac{1}{2} \times 5 \times h = \frac{5h}{2} \)

4. Set Up the Equation:
- According to the problem, the area of parallelogram ABCD is 8 times the area of triangle DPR:
\( AB \times h = 8 \times \left(\frac{5h}{2}\right) \)

5. Simplify the Equation:
- Simplifying the right side:
\( AB \times h = 8 \times \frac{5h}{2} = 20h \)
- Now, we can cancel h from both sides (assuming h ≠ 0):
\( AB = 20 \text{ cm} \)

6. Find CD:
- In a parallelogram, opposite sides are equal. Therefore, CD is equal to AB:
\( CD = AB = 20 \text{ cm} \)

Final Answer:
CD = 20 cm.