ABCD is a parallelogram, E and F are the mid-points of BC and CD. Find the ratio of area of parallelogram ABCD and ΔAEF
2:1
4:1
8:3
8:1
The correct Answer is:C
To find the ratio of the area of parallelogram ABCD to the area of triangle AEF, we can follow these steps:
Step 1: Understand the Configuration
- We have a parallelogram ABCD.
- Points E and F are the midpoints of sides BC and CD, respectively.
Step 2: Area of Parallelogram ABCD
- The area of a parallelogram can be calculated using the formula:
AreaABCD=base×height
- Let's denote the area of parallelogram ABCD as AABCD.
Step 3: Area of Triangle AEF
- Triangle AEF is formed by connecting points A, E, and F.
- To find the area of triangle AEF, we can use the fact that E and F are midpoints.
- The area of triangle AEF can be expressed in terms of the area of the parallelogram ABCD.
Step 4: Relationship Between Areas
- Since E and F are midpoints, triangle AEF is similar to triangles formed by the diagonals of the parallelogram.
- The area of triangle AEF is half of the area of triangle ACD because E and F divide the sides into equal halves.
- Therefore, we can express the area of triangle AEF as:
AAEF=14×AABCD
(This is because triangle AEF is one-fourth of the area of the parallelogram ABCD due to the midpoints.)
Step 5: Calculate the Ratio
- Now, we can find the ratio of the area of the parallelogram ABCD to the area of triangle AEF:
Ratio=AABCDAAEF=AABCD14AABCD=4
Step 6: Final Ratio
- Therefore, the ratio of the area of parallelogram ABCD to the area of triangle AEF is:
Ratio=4:1
Summary
- The ratio of the area of parallelogram ABCD to the area of triangle AEF is 4:1.
- We have a parallelogram ABCD.
- Points E and F are the midpoints of sides BC and CD, respectively.
- The area of a parallelogram can be calculated using the formula:
AreaABCD=base×height
- Let's denote the area of parallelogram ABCD as AABCD.
- Triangle AEF is formed by connecting points A, E, and F.
- To find the area of triangle AEF, we can use the fact that E and F are midpoints.
- The area of triangle AEF can be expressed in terms of the area of the parallelogram ABCD.
- Since E and F are midpoints, triangle AEF is similar to triangles formed by the diagonals of the parallelogram.
- The area of triangle AEF is half of the area of triangle ACD because E and F divide the sides into equal halves.
- Therefore, we can express the area of triangle AEF as:
AAEF=14×AABCD
(This is because triangle AEF is one-fourth of the area of the parallelogram ABCD due to the midpoints.)
- Now, we can find the ratio of the area of the parallelogram ABCD to the area of triangle AEF:
Ratio=AABCDAAEF=AABCD14AABCD=4
- Therefore, the ratio of the area of parallelogram ABCD to the area of triangle AEF is:
Ratio=4:1
- The ratio of the area of parallelogram ABCD to the area of triangle AEF is 4:1.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, the area of parallelogram ABCD is
 AAB×BMBBC×BNCDC×DLDAD×DL
AAB×BMBBC×BNCDC×DLDAD×DLABCD is a parallelogram P and R are two points on AB such that the area of parallelogram ABCD is 8 times the area of Δ DPR. If PR = 5 cm, then CD is equal to
A10 cmB5 cmC20 cmD12 cmABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AAN=√3ABBAN=2ABCAN2=32AB2DAN2=2AB2
ABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
View SolutionIn the given figure, ABCD is a rectangle; EandF are the mid-points of the sides BCandCD respectively. What is the ratio of the area of ΔAEF and that of ΔECF?
View SolutionIf ABCD is a parallelogram, E is the mid-point of AB and CE bisects ∠BCD, then ∠DEC is
View SolutionIn the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is
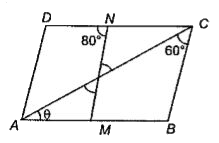
View SolutionIn the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is

View Solution
