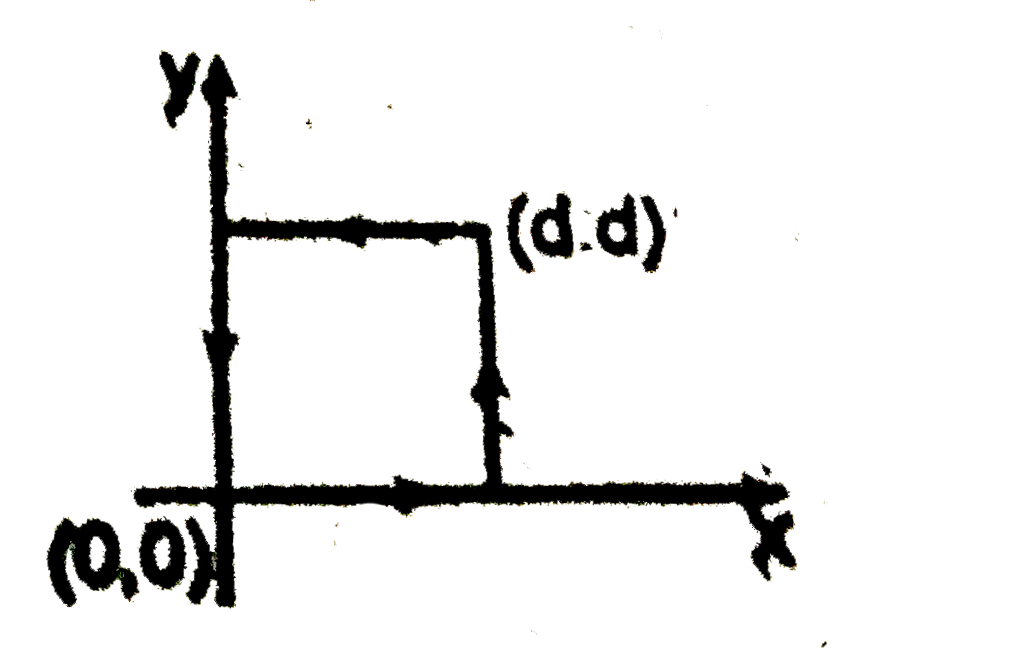
A particle moves in x-y plane from (0,0) to (a,a) and is acted upon by a force →F=k(y2ˆi+x2ˆj)N, where k is a constant and x and y are coordinates in meter. Find work done by this force, if the particle moves along
Two straight lines first from (0,0) to (a,0) and then from (a,0) to (a,a)
dW=→F.d→s=k(y2ˆi=x2ˆj).(dxˆi+dyˆj)
=ky2dx+kx2dy
When moves from (0,0) to (a,a) as shown in above figure, along path C which is a straight line for which y = x
⇒dy=dx
∴dW=kx2dx+kx2dx=2kx2dx
∴W=∫dW=2ka∫0x2dx=2ka33
In above illustration, the work done by the force is different for different paths for different paths taken, so it provides an example of non-conservative force.
Topper's Solved these Questions
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:SOLVED EXAMPLES
Explore 5 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:QUESTIONS FOR PRACTICE
Explore 25 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:Exercise - 3 Section-B
Explore 22 Videos
- WAVESBook:MOTIONChapter:WAVESExercise:EXERCISE -4 (Level -II) (previous year JEE Advanced)
Explore 10 Videos
Similar Questions
A force →F=xˆi+y2ˆjN acts on a particle and the particle moves from (1,2)m to (–3,4)m. Find work done by the force →F.
View SolutionA particle moving along the x- axis is subjected to a force given by F=F0(ex/a−1) where F0 and are constants Determine an expression for the work done by this force as the particle moves from the origin to the point x=r
View Solution
Knowledge Check
The work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
 AzeroBAdCAd2DAd3
AzeroBAdCAd2DAd3A force →F=k[yˆi+xˆj] where k is a positive constant acts on a particle moving in x-y plane starting from the point (3, 5), the particle is taken along a straight line to (5, 7). The work done by the force is :
AzeroB35 KC20 KD15 KA particle is moved from (0,0) to (a, a) under a force →F=(3ˆi+4ˆj) from two paths. Path 1 is OP and path 2 is OQP. Let W and W be the work done by this force in these two paths.Then
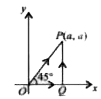 AW = W2BW = 2WCW = 2WDW = 4W
AW = W2BW = 2WCW = 2WDW = 4W
A force F=α+βx acts on a particle of mass m along the X . Axis . Here αandβ are constants . Find the work done by this force when particle moves form x = 0 to x = d .
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
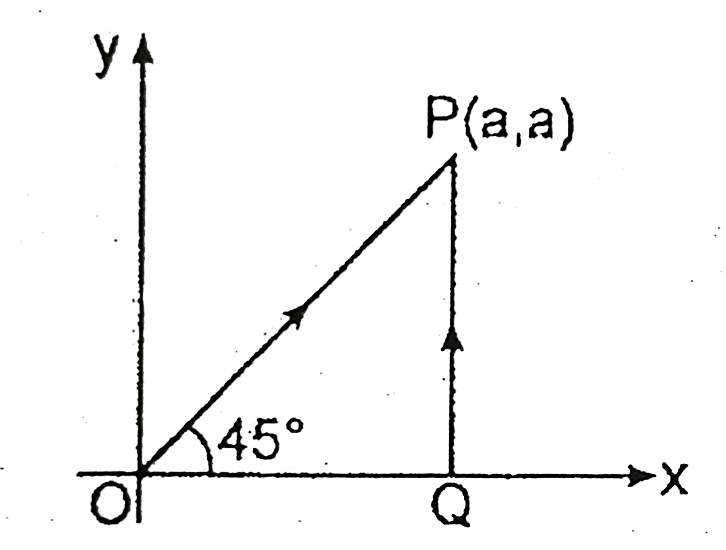
View SolutionA particle is movbed from (0,0)→(a,a) under a force F=(x2ˆi+y3ˆj) from two paths. Path 1 si OP and Path 2 is OQP. Let W1 and W2 be the work done by this force in these two paths. Then
View SolutionA body is displaced from (0,0) to (1m,1m) along the path x=y by a force F=(x2ˆj+yˆi)N. The work done by this force will be
View SolutionA force F=20+10y acts on a particle in y-direction where F is in Newton and y in meter. Wrok done by this force to move the particle from y=0 to y=1m is:
View Solution