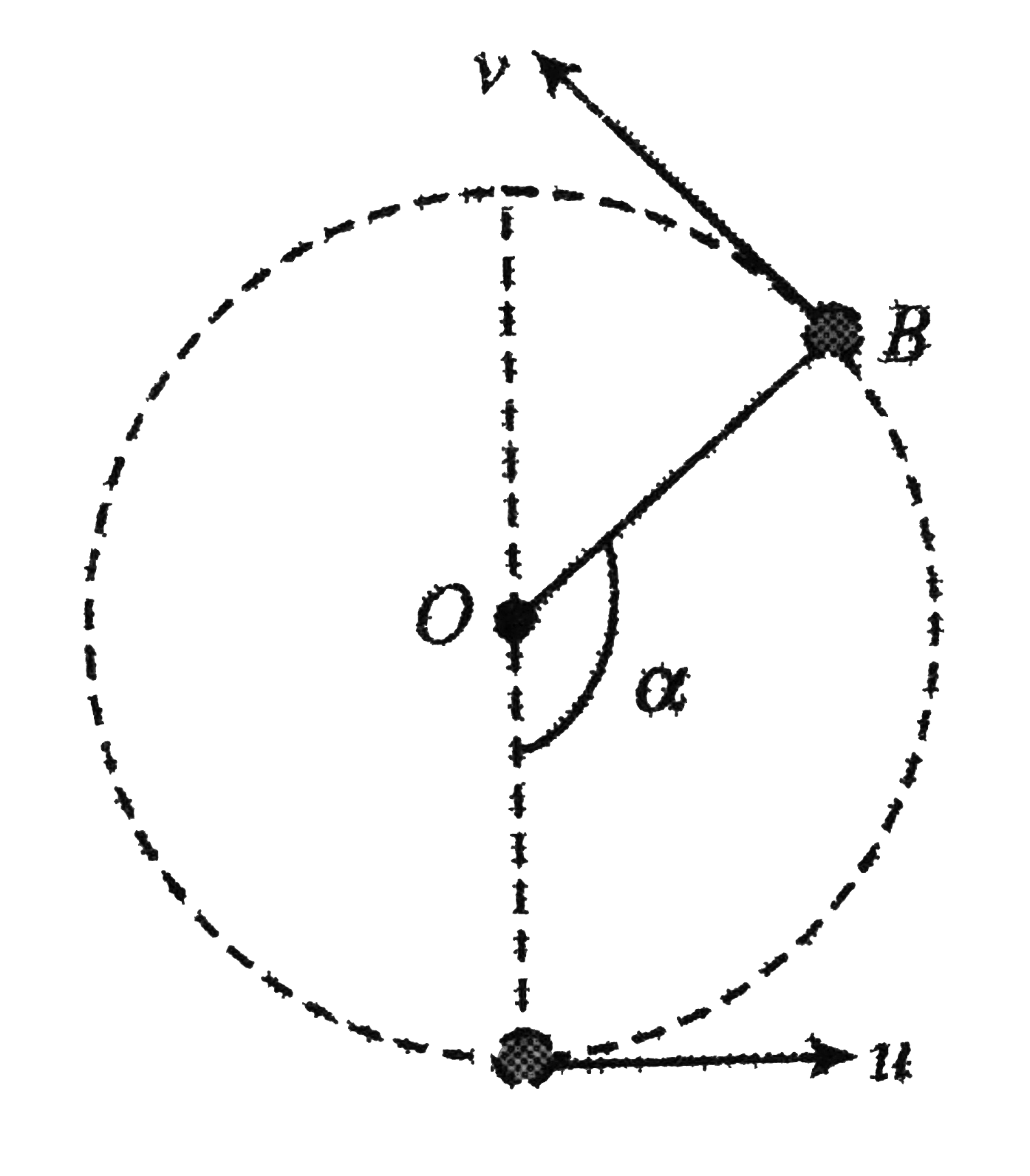
The bob of a simple pendulum is given a sharp hit impart it a horizontal speed of $\sqrt{3 g L}$ . Find an angle made by the string with the upper verticle before it becomes slack. Also, calculate the maximum height attained by the bob above the point of suspension. $L$ is length of the string.

Video Solution

Text Solution

Verified by Experts

Now, after slackening of the string, the motion of the bob is under gravity only, for which the maximum height from P is given by
$h_{2} = \frac{v^{2} {sin}^{2} α}{2 g}$
where $v^{2} = \frac{g l}{3} and {sin}^{2} α = 1 - {cos}^{2} α = 1 - {(\frac{1}{3})}^{2} = \frac{8}{9}$
$∴ h_{2} = \frac{(\frac{g l}{3}) (\frac{8}{9})}{2 g} = \frac{4 l}{27}$
$∴$ maximum height from A is = $h_{1} + h_{2}$
$= l (1 + \frac{1}{3}) + \frac{4 l}{27} = \frac{40 l}{27}$

Updated on:21/07/2023

A simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal accelertion a. The angle made by the string with verical is
A ${tan}^{- 1} (\frac{a}{g})$
B ${tan}^{- 1} (1 - \frac{a}{g})$
C ${cos}^{- 1} (\frac{a}{g})$
D ${sin}^{- 1} (\frac{a}{g})$
A simple pendulum is released from rest at the horizontally stretched position. When the string makes an angle $θ$ with the vertical, the angle $θ$ which the acceleration vector of the bob makes with the string is given by–

A $ϕ = 0$
B $φ = {tan}^{- 1} (\frac{tan θ}{2})$
C $φ = {tan}^{- 1} (2 tan θ)$
D $φ = π / 2$
The length of a simple pendulum is $1 m$ . The bob is given a velocity $7 m s^{- 1}$ in horizontal direction from mean position. During upward motion of bob, if the string breaks when the bob is horizontal, then the maximum vertical height of ascent of bob from rest position is
A $2.5 m$
B2 m
C3 m
D $3.5 m$