A force →F=xˆi+y2ˆjN acts on a particle and the particle moves from (1,2)m to (–3,4)m. Find work done by the force →F.
To find the work done by the force →F=x^i+y2^jN as the particle moves from the point (1,2)m to (−3,4)m, we can follow these steps:
Step 1: Understand the Work Done Formula
The work done W by a force along a path can be expressed as:
W=∫→F⋅d→s
where d→s is the differential displacement vector.
Step 2: Express the Differential Displacement
The differential displacement d→s can be expressed in terms of its components:
d→s=dx^i+dy^j
Step 3: Substitute the Force and Displacement
Now, substituting the expressions for →F and d→s:
dW=→F⋅d→s=(x^i+y2^j)⋅(dx^i+dy^j)=xdx+y2dy
Step 4: Set Up the Integral for Work Done
To find the total work done, we will integrate dW:
W=∫(xdx+y2dy)
Step 5: Determine the Limits of Integration
The particle moves from (1,2) to (−3,4). We will handle the integration in two parts:
1. For x from 1 to −3
2. For y from 2 to 4
Step 6: Calculate the Integral
We can separate the integral:
W=∫−31xdx+∫42y2dy
Calculating the first integral:
∫xdx=x22∣∣−31=(−3)22−(1)22=92−12=82=4
Calculating the second integral:
∫y2dy=y33∣∣42=(4)33−(2)33=643−83=563
Step 7: Combine the Results
Now, combine the results of both integrals:
W=4+563
To combine these, convert 4 into a fraction with a denominator of 3:
4=123
Thus,
W=123+563=683J
Final Answer
The work done by the force →F is:
W=683J
The work done W by a force along a path can be expressed as:
W=∫→F⋅d→s
where d→s is the differential displacement vector.
The differential displacement d→s can be expressed in terms of its components:
d→s=dx^i+dy^j
Now, substituting the expressions for →F and d→s:
dW=→F⋅d→s=(x^i+y2^j)⋅(dx^i+dy^j)=xdx+y2dy
To find the total work done, we will integrate dW:
W=∫(xdx+y2dy)
The particle moves from (1,2) to (−3,4). We will handle the integration in two parts:
1. For x from 1 to −3
2. For y from 2 to 4
We can separate the integral:
W=∫−31xdx+∫42y2dy
∫xdx=x22∣∣−31=(−3)22−(1)22=92−12=82=4
∫y2dy=y33∣∣42=(4)33−(2)33=643−83=563
Now, combine the results of both integrals:
W=4+563
4=123
Thus,
W=123+563=683J
The work done by the force →F is:
W=683J
Topper's Solved these Questions
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:SOLVED EXAMPLES
Explore 5 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:QUESTIONS FOR PRACTICE
Explore 25 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:Exercise - 3 Section-B
Explore 22 Videos
- WAVESBook:MOTIONChapter:WAVESExercise:EXERCISE -4 (Level -II) (previous year JEE Advanced)
Explore 10 Videos
Similar Questions
If force →f=(3x→i+y2) W is acting on a body and body moves from (1m, 2m, 1m) to (2m, 3, 8m), then find the work done due to the force
View SolutionA particle is acted upon by a force →F=yˆi+xˆj newton. When the particle is moved from (1 m, 1 m) to (9m, 3 m) via straight path, work done by →F is y. What is the value of xy?
View Solution
Knowledge Check
A force given by →F=fxˆi+fyˆj+fzˆk acts on a particle which moves from (a, b, c) to (d, e, f). The work done by the force F is : (Here A1,A2,A3 are magntitude of area bounded )
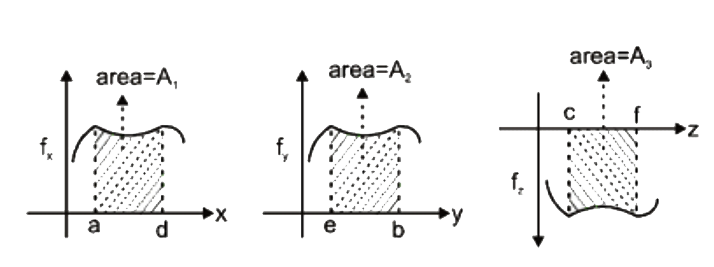 AA1+A2+A3BA1−A2−A3C−A1+A2−A3DA1−A2+A3
AA1+A2+A3BA1−A2−A3C−A1+A2−A3DA1−A2+A3A force of (4x2+3x)N acts on a particle which displaces it from x=2m to x=3m. The work done by the force is
A32.8JB3.28JC0.328JDZeroConsider a force →F=−xˆi+yˆj. The particle is moved from point A(1,0) to B(0,1) along the line segment. The work done by force is (All quantities are in Si units)
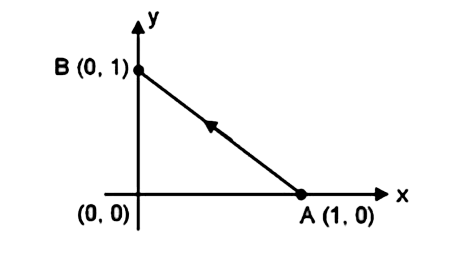 A12B32C2D1
A12B32C2D1
In a two dimensional space the potential energy function for a conservative force acting on a particle of mass m = 0.1 kg is given by U = 2 (x + y) joule (x and y are in m). The particle is being moved on a circular path at a constant speed of V=1ms−1. The equation of the circular path is x2+y2=42. (a) Find the net external force (other than the conservative force) that must be acting on the particle when the particle is at (0, 4). (b) Calculate the work done by the external force in moving the particle from (4, 0) to (0, 4).
View SolutionA force →F=(3x2+2x−7)N acts on a 2 kg body as a result of which the body gets displaced from x=0 to x=5m. The work done by the force will be –
View SolutionA force →F=(3ˆi+4ˆj) N acts on a body and displaces it by →S=(3ˆi+4haj)m. The work done (W= →F⋅→S) by the force is :
View SolutionForce acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
Now consider another situation. A force →F=(4ˆi+3ˆj)N acts on a particle of mass 2kg. The particle under the action of this force moves from the origin to a point A (4m,−8m). Initial speed of the particle, i.e., its speed at the origin is 2√6ms−1. Figure shows three paths for the motion of the particle from O to A.

Speed of the particle at A will be nearly
View SolutionForce acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
Now consider another situation. A force →F=(4ˆi+3ˆj)N acts on a particle of mass 2kg. The particle under the action of this force moves from the origin to a point A (4m,−8m). Initial speed of the particle, i.e., its speed at the origin is 2√6ms−1. Figure shows three paths for the motion of the particle from O to A.
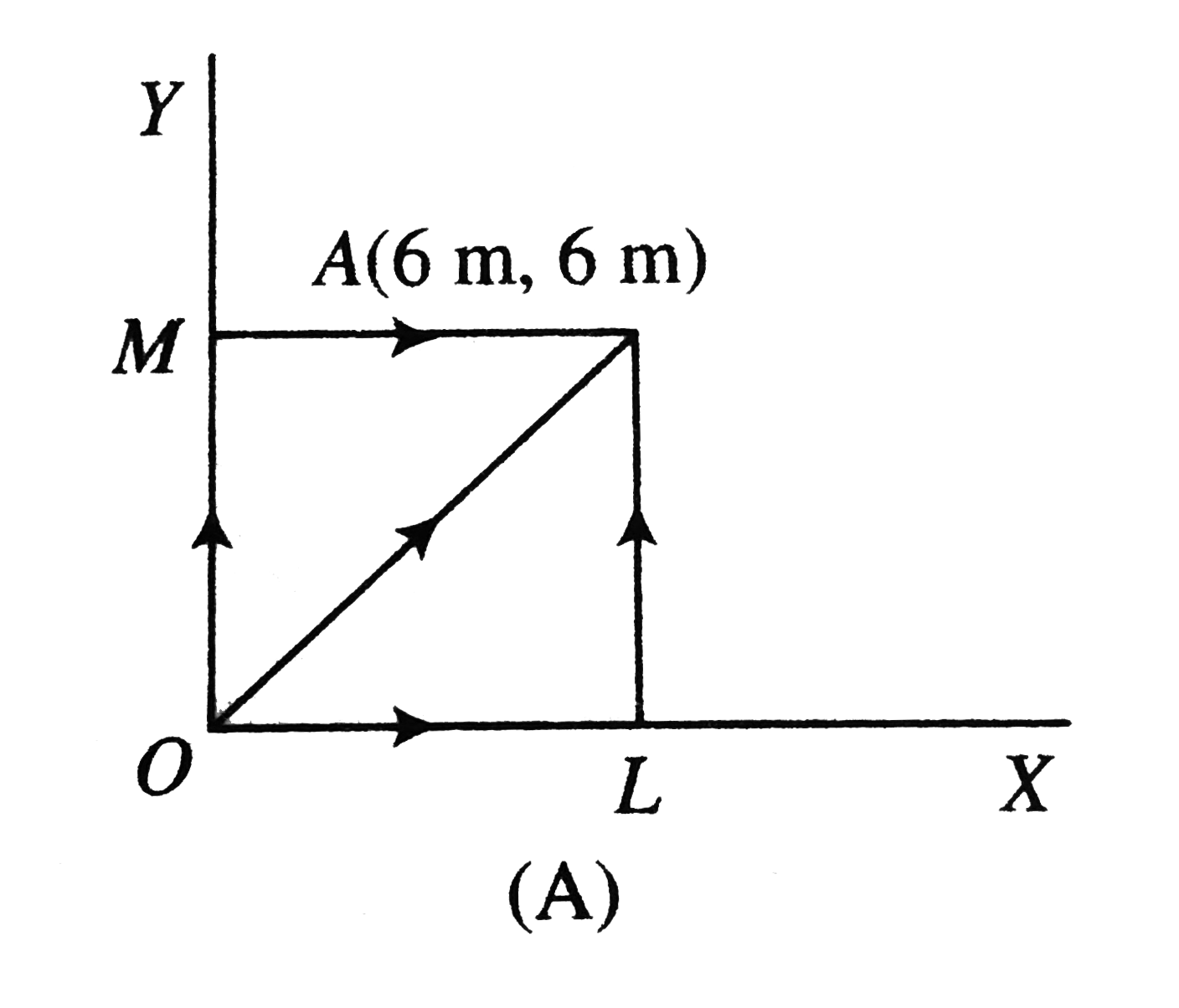
If the potential energy at O is 16J, the potential energy at A will be
View Solution

