A uniform rod of mass M and length L is held vertically upright on a horizontal surface as shown in figure. Assuming zero potential energy at the base of the rod, determine the potential energy of the rod.
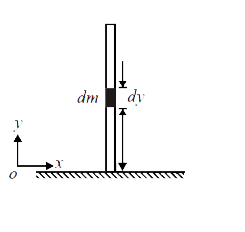
Since the parts of the rod are at different level with respect to the horizontal surface, therefore, we have to use the integration to find its potential energy. Consider a small element of length dy at a height y from the horizontal. Mass of the element is
dm=MLdy
Its potential energy is given by
dU=(dm)gy
or dU=MLgydy
On integration, we get
U=MgLL∫0ydy
or U=MgL∣∣∣y22∣∣∣L0
or U=12MgL
Note that the potential energy of the rod is equal to the product of Mg and height of the center of mass (L2) from the surface.
Topper's Solved these Questions
- WORK, POWER & ENERGY BOOK - MOTIONCHAPTER - WORK, POWER & ENERGY EXERCISE - SOLVED EXAMPLES
5 Videos
- WORK, POWER & ENERGY BOOK - MOTIONCHAPTER - WORK, POWER & ENERGY EXERCISE - QUESTIONS FOR PRACTICE
25 Videos
- WORK, POWER & ENERGY BOOK - MOTIONCHAPTER - WORK, POWER & ENERGY EXERCISE - Exercise - 3 Section-B
22 Videos
- WAVESBOOK - MOTIONCHAPTER - WAVESEXERCISE - EXERCISE -4 (Level -II) (previous year JEE Advanced)
10 Videos
Similar Questions
A uniform rod of mass M and length L is standing vertically along the y-axis on a smooth horizontal surface as shown. A small disturbance causes the lower end to slip on the smooth horizontal surface and rod starts falling. The path followed by centre of mass of the rod during the fall is

View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View Solution
Knowledge Check
A uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :A7F2L6AYB11F2L6AYC5F2L6AYD3F2L2AY
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:A12mVLcosθB13mVLsinθCmVLsincosθDzeroA rod of mass M and length L is made to stand vertically. Potential energy of the rod in this position is
AMglBMgl2CMgl3DMgl4
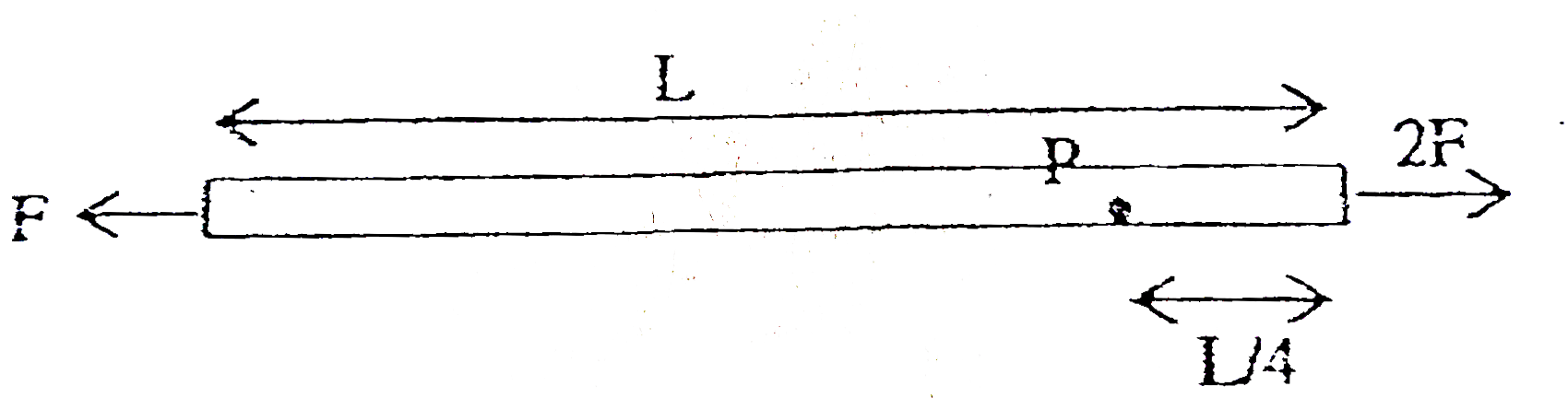
A uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Ratio of elastic potential energy stored in section PQ and section QR of the rod is
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

View SolutionA uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.

Distance travelled by the centre of the rod, while rod rotates by 90∘
View Solution
