A particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
Let it rotates by angle α
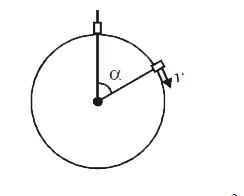
mgcosα−N=mv2R

It looses contact i.e. N = 0
⇒mgcosα=mv2R
=v2=gRcosα ....(i)
Also applying work energy theorem
mgh=12m(v2−0)
⇒mgR(1−cosα)=12m(gRcosα−0)
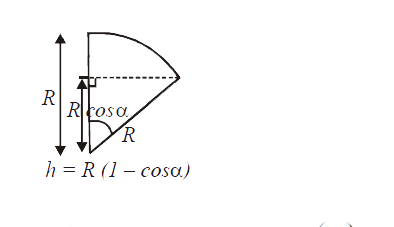
⇒cosα=13⇒α=cos−1(13)
Also from equation (i), v=√gR3
Topper's Solved these Questions
- WORK, POWER & ENERGY BOOK - MOTIONCHAPTER - WORK, POWER & ENERGY EXERCISE - SOLVED EXAMPLES
5 Videos
- WORK, POWER & ENERGY BOOK - MOTIONCHAPTER - WORK, POWER & ENERGY EXERCISE - QUESTIONS FOR PRACTICE
25 Videos
- WORK, POWER & ENERGY BOOK - MOTIONCHAPTER - WORK, POWER & ENERGY EXERCISE - Exercise - 3 Section-B
22 Videos
- WAVESBOOK - MOTIONCHAPTER - WAVESEXERCISE - EXERCISE -4 (Level -II) (previous year JEE Advanced)
10 Videos
Similar Questions
A particle is released from the top of a smooth hemisphere.find the angle rotated by the radius through the particle, when it loses contract with the hemisphere. Also sketch variation of normal contact force with cosθ, where θ is an angle rotated by the radius through the particle.
View SolutionA particle of mass m is kept on a fixed , smooth sphere of radius R at a position, where the rdius thrugh the particle makes an angle of 300 with the vertical. The particle is releases from this positon. a. What is the force exerted by the sphere on teh particle just after the release? b. Find the distance travelled by the particle before it leaves contact with the sphere.
View SolutionParticle slides down the surface of a smooth fixed sphere of radius r starting from rest at the highest point. Find where it will leave the sphere. Show that it strike the horizontal plane through the lowest point of the sphere at a distance equal to 5[√5+4√2](r/27) from the vertical diameter.
View SolutionA particle slides down the surface of a smooth fixed sphere of radius R starting from rest at the highest point B. Particle leaves the sphere at some point and then strikes the horizontal plane passing through the lowest point A of the sphere at point P. The distance AP is given by
AP=n27[√n+4√2]R where 'n' is an integer, find n (Take g=10m/s2)

View SolutionA particle of mass m is released on a fixed. Smooth sphere of radius R at a position, where the radius through the particle makes an angle of α with the verticle. What is the angle made by radius through the particle when the particle loses contact with sphere? (cosα=3/4)
View SolutionA particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.

View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionA particle of mass m is kept on the top of a smooth sphere of radius LR. It is given a sharp impulse whichimparts it a horizontal speed v. a. find thenormal force between the sphere and the particle just after the impulse. B. What should be the minimum value of v for which the particle does not slip on the sphere? c. Assuming the velocity v to be half the minimum calculated in part, d. find teh angle made by the radius through the particle with the vertical when it leaves the sphere.

View SolutionA small box of mass m is placed on the outer surface of a smooth fixed sphere of radius R at a point where the radius makes a angle Pse with the vertical. The box is released from this position. Find the distance travelled by the box before it leaves contact with the sphere.
View SolutionA particle of mass m being to slide down a fixed smooth sphere from the top as shown. If its acceleration when it breaks off the sphere is 2a. The value of a is :
View Solution
