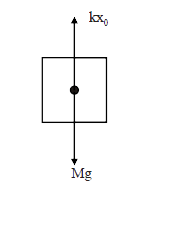
A sping of spring constant k is attached to the ceiling. A block of mass M is attached to its lower end and is released suddenly.
(ii) Find its speed at the instant it passes throught the equilibrium position.
When the block is equilibrium (i.e. Fnet=0)
kx∘=Mg
⇒x0=Mgk
∴ Applying work energy therom for motion from (a) to (b)
Mgx0−12kx20=12M(V20−0)
⇒Mg(Mgk)−12k(Mgk)2=12MV20
⇒v0=g√Mk
Topper's Solved these Questions
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:SOLVED EXAMPLES
Explore 5 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:QUESTIONS FOR PRACTICE
Explore 25 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:Exercise - 3 Section-B
Explore 22 Videos
- WAVESBook:MOTIONChapter:WAVESExercise:EXERCISE -4 (Level -II) (previous year JEE Advanced)
Explore 10 Videos
Similar Questions
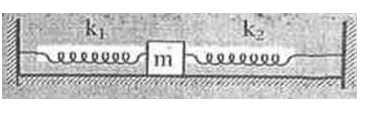
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.

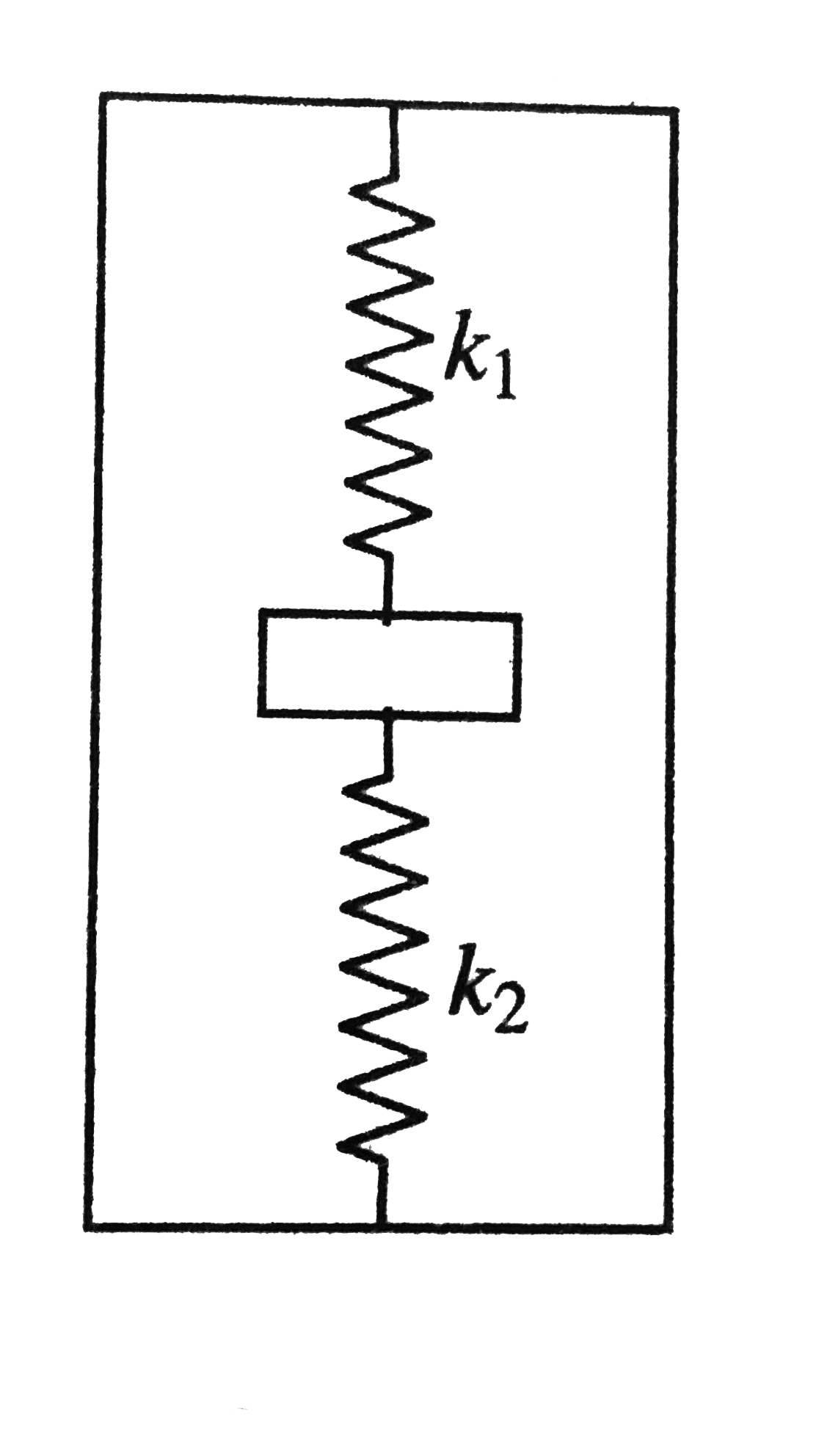
View SolutionOne end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
View Solution
Knowledge Check
An ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
A(a) 4MgkB(b) 2MgkC(c) MgkD(d) Mg2kAn ideal spring with spring - constant K is bung from the colling and a block of mass M is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
A4MgKB2MgKCMgKDMg4KA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
View SolutionA block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
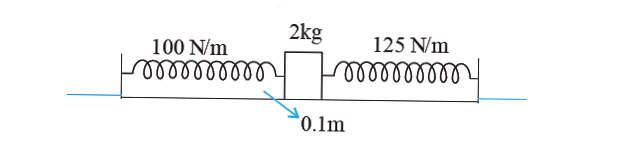
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionAn ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
View Solution

