Particle slides down the surface of a smooth fixed sphere of radius r starting from rest at the highest point. Find where it will leave the sphere. Show that it strike the horizontal plane through the lowest point of the sphere at a distance equal to 5[√5+4√2](r/27) from the vertical diameter.
The correct Answer is:A
Step by step video, text & image solution for Particle slides down the surface of a smooth fixed sphere of radius r starting from rest at the highest point. Find where it will leave the sphere. Show that it strike the horizontal plane through the lowest point of the sphere at a distance equal to 5[sqrt(5)+4sqrt(2)](r//27) from the vertical diameter. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ
158 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
A particle slides down the surface of a smooth fixed sphere of radius R starting from rest at the highest point B. Particle leaves the sphere at some point and then strikes the horizontal plane passing through the lowest point A of the sphere at point P. The distance AP is given by
AP=n27[√n+4√2]R where 'n' is an integer, find n (Take g=10m/s2)

View SolutionA particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
View Solution
Knowledge Check
A particle moving on the inside of a smooth sphere of radius r describing a horizontal circle at a distance r/2 below the centre of the sphere. What is its speed ?
A√5grB√4gr/3C√3gr/2D√√3grA unofrom rope of mass m is placeced on a smooth fixed sphere of radius R as shown in the figure .Find the tension T in the rope when it is in a horizontal plane at a vertical distance h=R/2 below the top of the sphere .
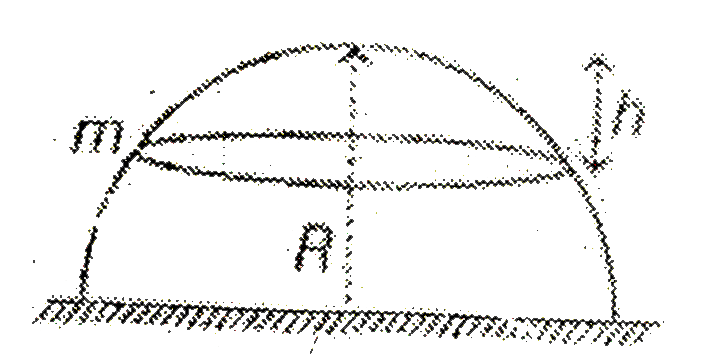 Amg2πBmg2C√3mg2D√3mg2π
Amg2πBmg2C√3mg2D√3mg2πA skier plans to ski a smooth fixed hemisphere of radius R He starts from rest from a curved smooth surface of height (R/4) the angle θ at which he leaves the hemisphere is
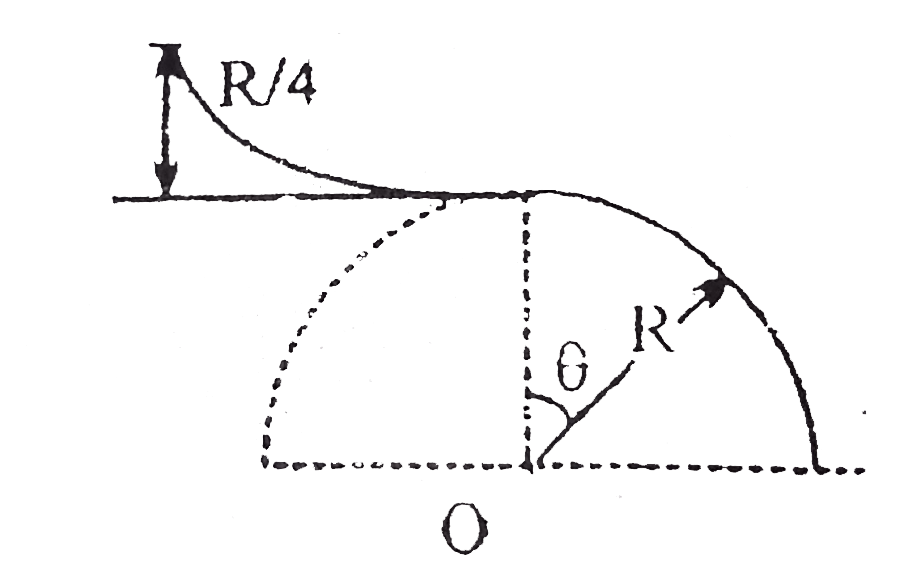 Acos−1(2/3)Bcos−1(5/√3Ccos−1(5/6)Dcos−1(5/2√3
Acos−1(2/3)Bcos−1(5/√3Ccos−1(5/6)Dcos−1(5/2√3
The centre of neutral conducting sphere of radius "R" is at distance 'd' from a point charge "Q" .The potential of the sphere is
View SolutionA particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
View SolutionA skier plane to ski a smooth fixed hemisphere of radius R . He starts from rest from a curve smooth surface of height (R4) . The angle θ at which he leaves the hemisphere is
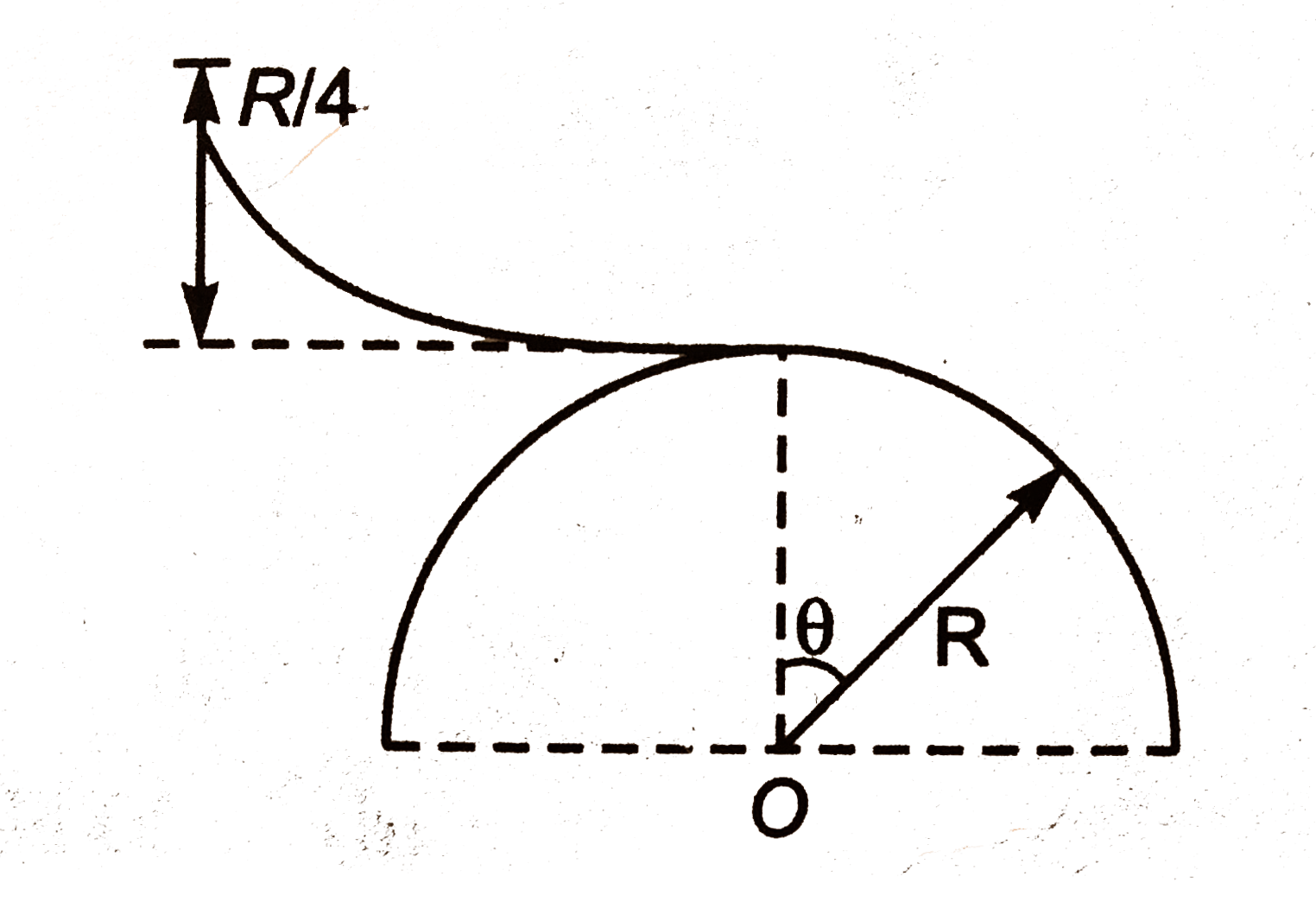
View SolutionIf charge q induced on outer surface of sphere of radius R, then intensity at point P at distance S from centre is
View SolutionIf charge q is induced on outer surface of sphere of radius R, then intensity at a point P at a distance S from its centre is
View Solution
