A smooth rubber cord of length whose coefficient of elasticity is k is suspended by one end from the point O (figure). The other end is fittetd with a catch B. A small sleeve A of mass m starts falling from the point O. Neglecting the masses of the thread and the catch, find the maximum elongation of the cord.
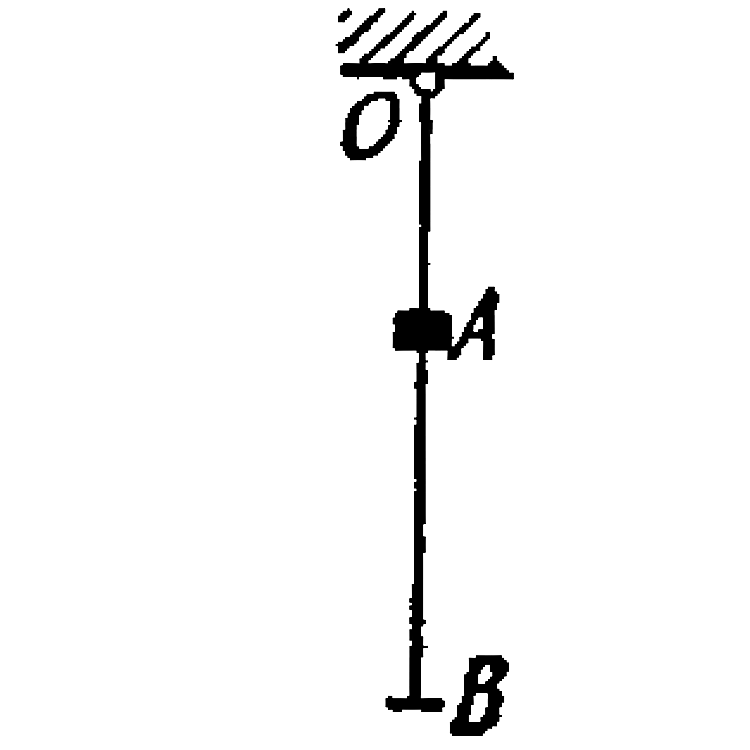
The correct Answer is:A, B
Step by step video, text & image solution for A smooth rubber cord of length l whose coefficient of elasticity is k is suspended by one end from the point O (figure). The other end is fittetd with a catch B. A small sleeve A of mass m starts falling from the point O. Neglecting the masses of the thread and the catch, find the maximum elongation of the cord. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:PHYSICS GALAXY - ASHISH ARORAChapter:WORK, ENERGY AND POWERExercise:unsolved
Explore 1 Video
- WORK, ENERGY AND POWERBook:PHYSICS GALAXY - ASHISH ARORAChapter:WORK, ENERGY AND POWERExercise:MCQ
Explore 158 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Unsolved Numerical
Explore 63 Videos
Similar Questions
A rubber string of mass m and rigidity k is suspended at one end. Determine the elongation Δl of the string.
View SolutionA smooth uniform rod AB of mass M and length l rotates freely with an angular velocity ω0 in a horizontal plane about a stationary vertical axis passing through its end A. A small sleeve of mass m starts sliding along the rod from the point A. Find the velocity v′ of the sleeve relative to the rod at the moment it reaches its other and B.
View Solution
Knowledge Check
An elastic cord of constant K and length L is hung from point A having a massless lock at the other end. A smooth ring of mass M falls from point A , the maximum elongation of cord is
 AmgK(1+1+2KLMg)BMgK(1−(1−2KLMg)1/2)CMgLKDMgK(1+(1+2KLMg)1/2)
AmgK(1+1+2KLMg)BMgK(1−(1−2KLMg)1/2)CMgLKDMgK(1+(1+2KLMg)1/2)A block of mass m falls from a height h onto the end of a platform as shown in figure. The springis initially unstreched and the mass of the platform on be neglected. Assuming if there is no loss of energy, the maximum elongation of the spring is
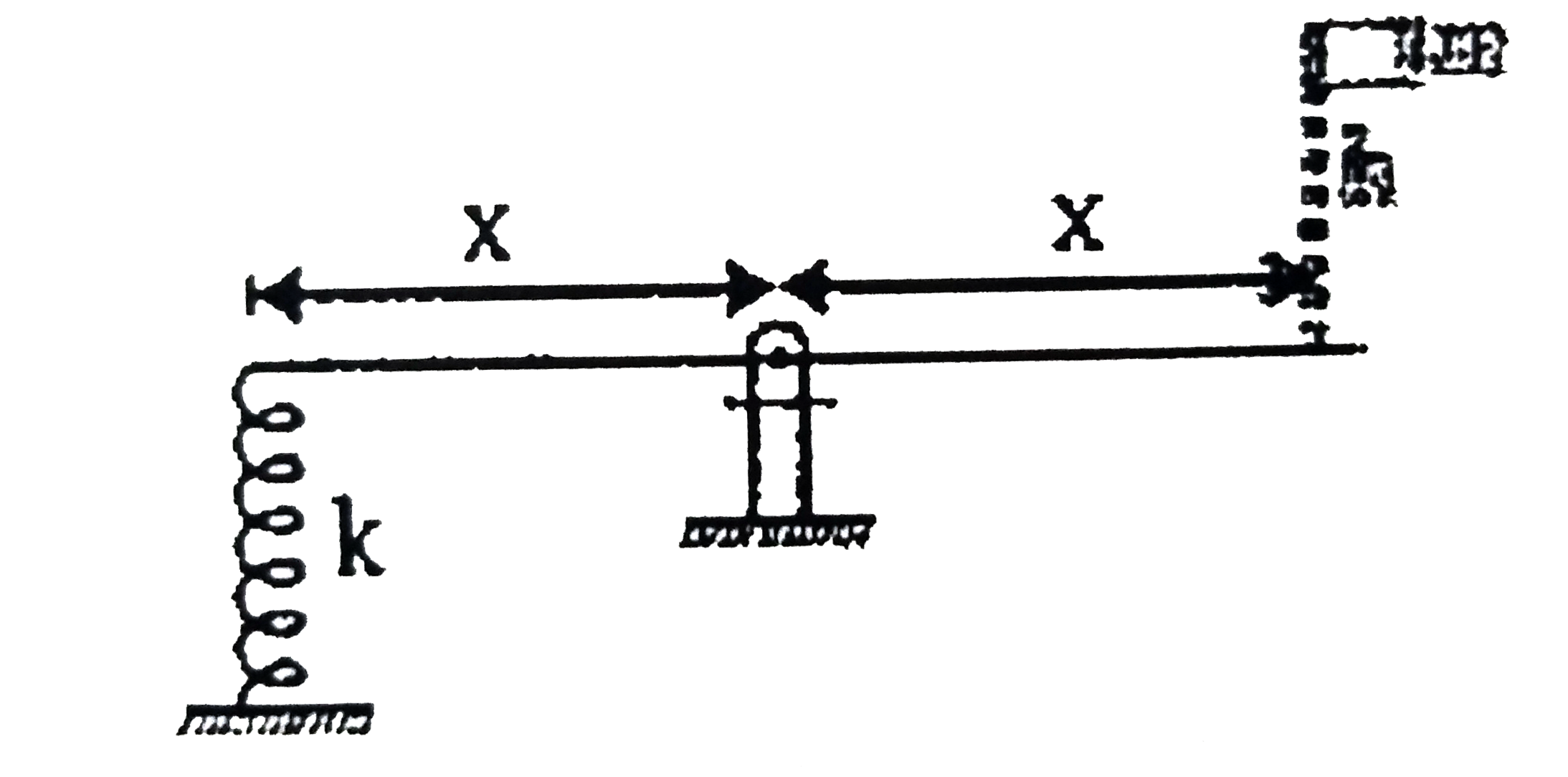 Amg+√m2g2+2mghKKBmg+√m2g2−2mghkKCK√m2g2+2mghkD√m2g2+2mghkK
Amg+√m2g2+2mghKKBmg+√m2g2−2mghkKCK√m2g2+2mghkD√m2g2+2mghkKA small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω.
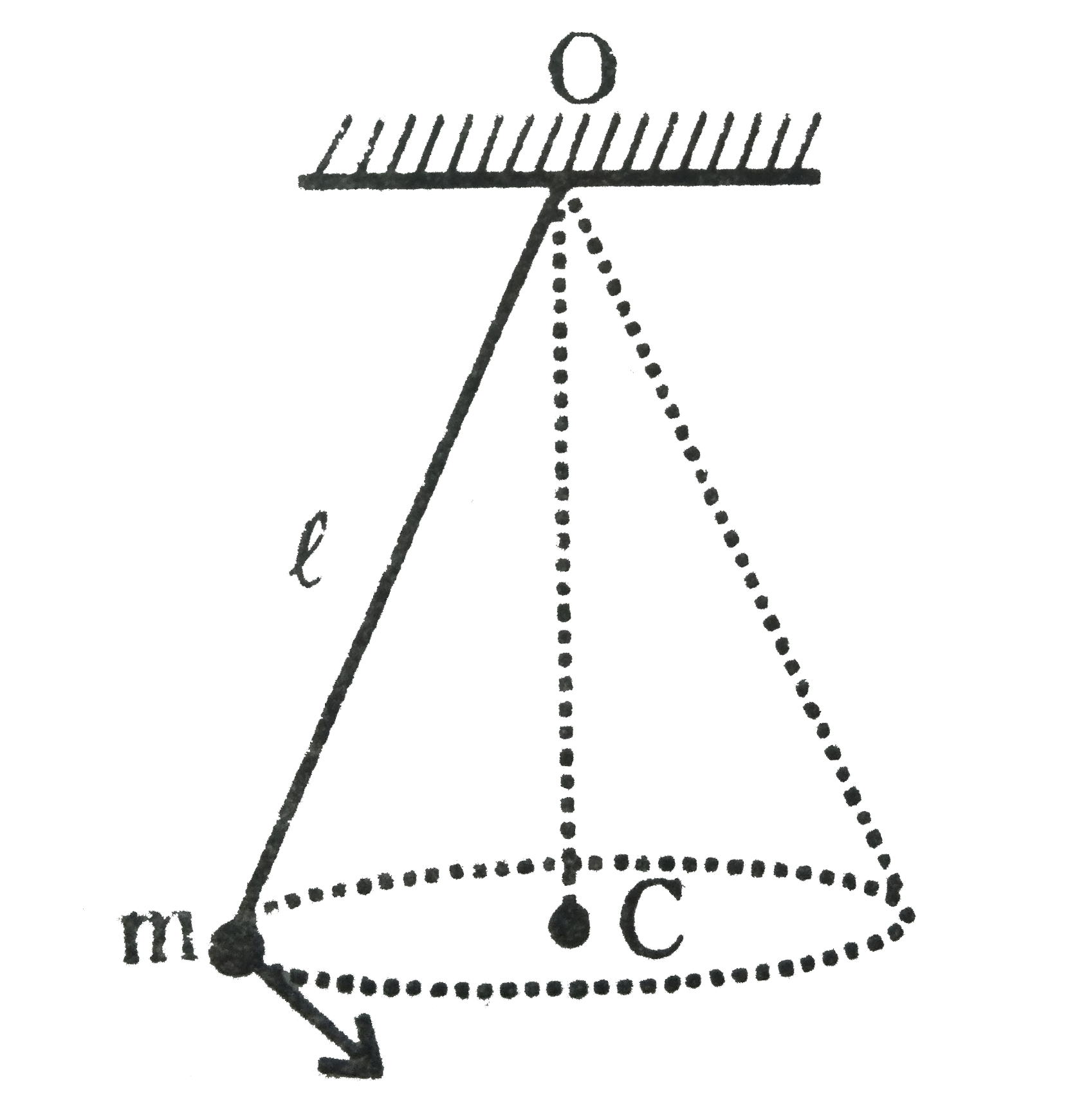 .Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conserved
.Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conserved
A light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.

View SolutionA weight is suspended from a thread of length l. What is the initial speed that has to be imparted to it at the lowest point to make it complete a full revolution? The mass of the thread is to be neglected.
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionThe mass of an uniform ladder of length l increases uniformly from one end A to the other end B,
find the position of the centre of mass from end A.
View Solution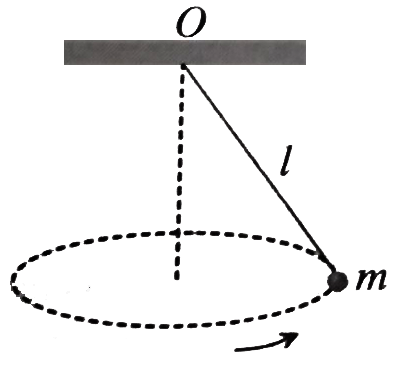
A point mass m is suspended from a light thread of length l, fixed at O, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass are
View Solution