A rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

(mg)24k
(mg)22k
(mg)28k
(mg)2k.
The correct Answer is:C
∑(Moment aboutO)=0
∴(kx)l=mg(l2) or x=mg2k
U=12kx2=(mg)28k
Similar Questions
A block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA body of mass m hangs by an inextensible string that passes over a smooth mass less pulley that is fitted with a light spring of stiffness k as shown in figure. If the body is released from rest and the spring is released, calculate the maximum elongation of the spring.
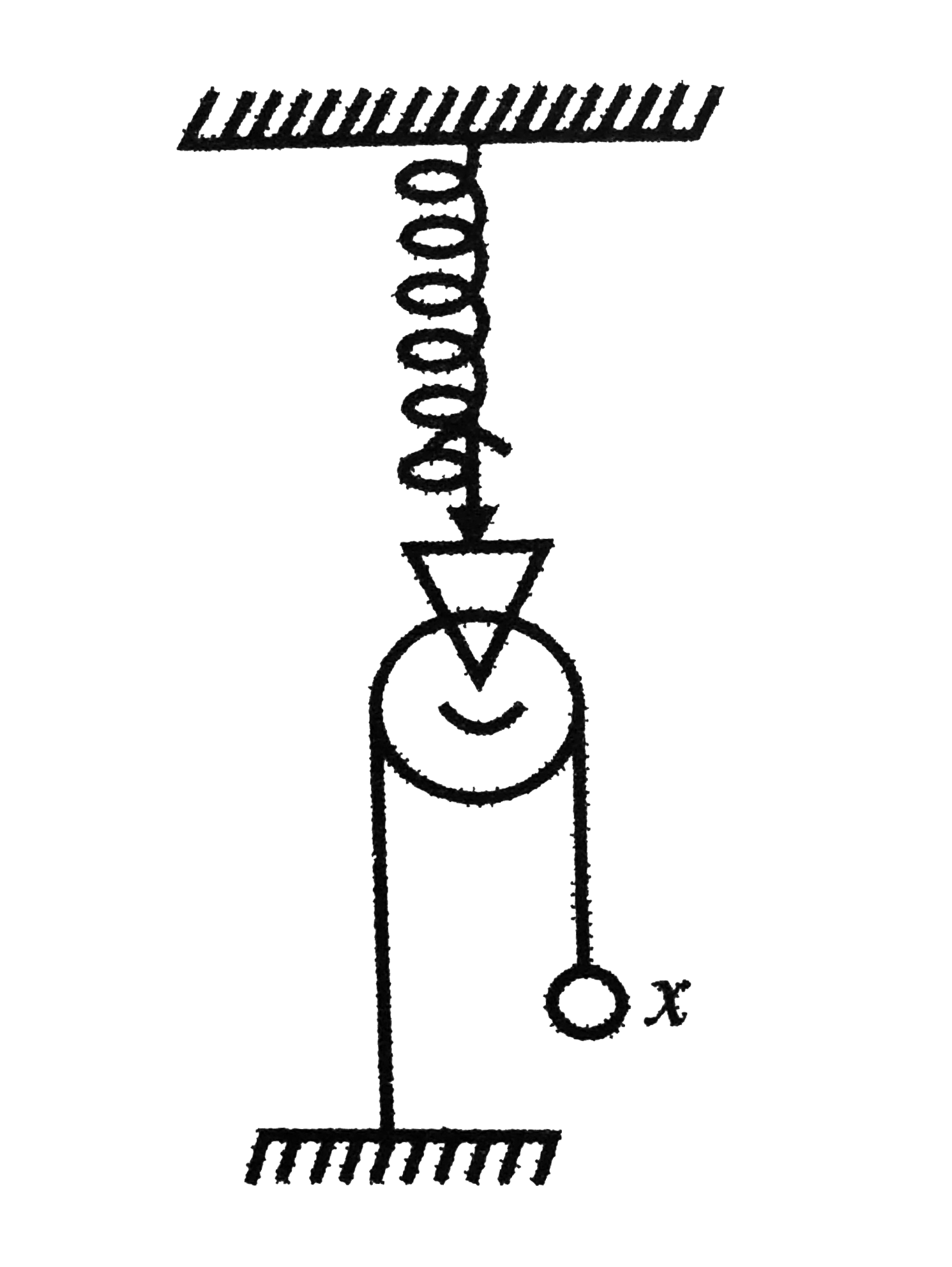
View Solution
Knowledge Check
A force of 10 N holds an ideal spring with a 20Nm spring constant in compression. The potential energy stored in the spring is
A0.5JB2.5JC5JD10 JTwo springs are in a series combination and are attached to a block of mass 'm' which is in equilibrium. The spring constants and extension in the springs are as shown in the figure. Then the force exerted by the spring on the block is :
 Ak1k2k1+k2(x1+x2)Bk1x1+k2x2Ck1x1DNone of these
Ak1k2k1+k2(x1+x2)Bk1x1+k2x2Ck1x1DNone of theseA rod of mass 'M' and length'
L' is hinged about one end and a
particle of mass 'M' is
attached to its other end If it is
kept horizontal with the help of
a spring of spring constant 'K'
as shown in fig. find the
extension in spring :-
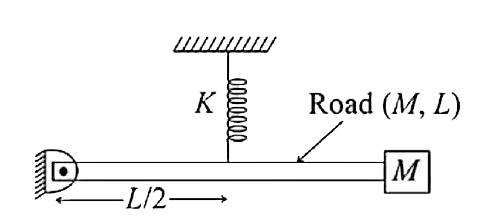 A3MgKBMgKC2MgKD4MgK
A3MgKBMgKC2MgKD4MgK
A uniform rod AB has mass M and length L. It is in equilibrium supported in vertical plane by three identical springs as shown in figure. The springs are connected at A, C and D such that AC=CD=L3. Assume that the springs are very stiff and the angle a made by the rod with the horizontal in equilibrium position is very small. (All springs are nearly vertical). Calculate the tension in the three springs.
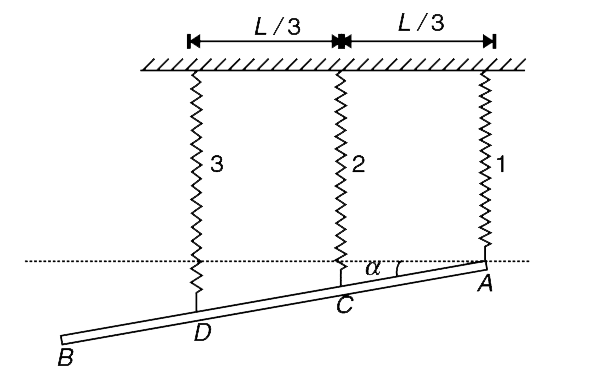
View Solution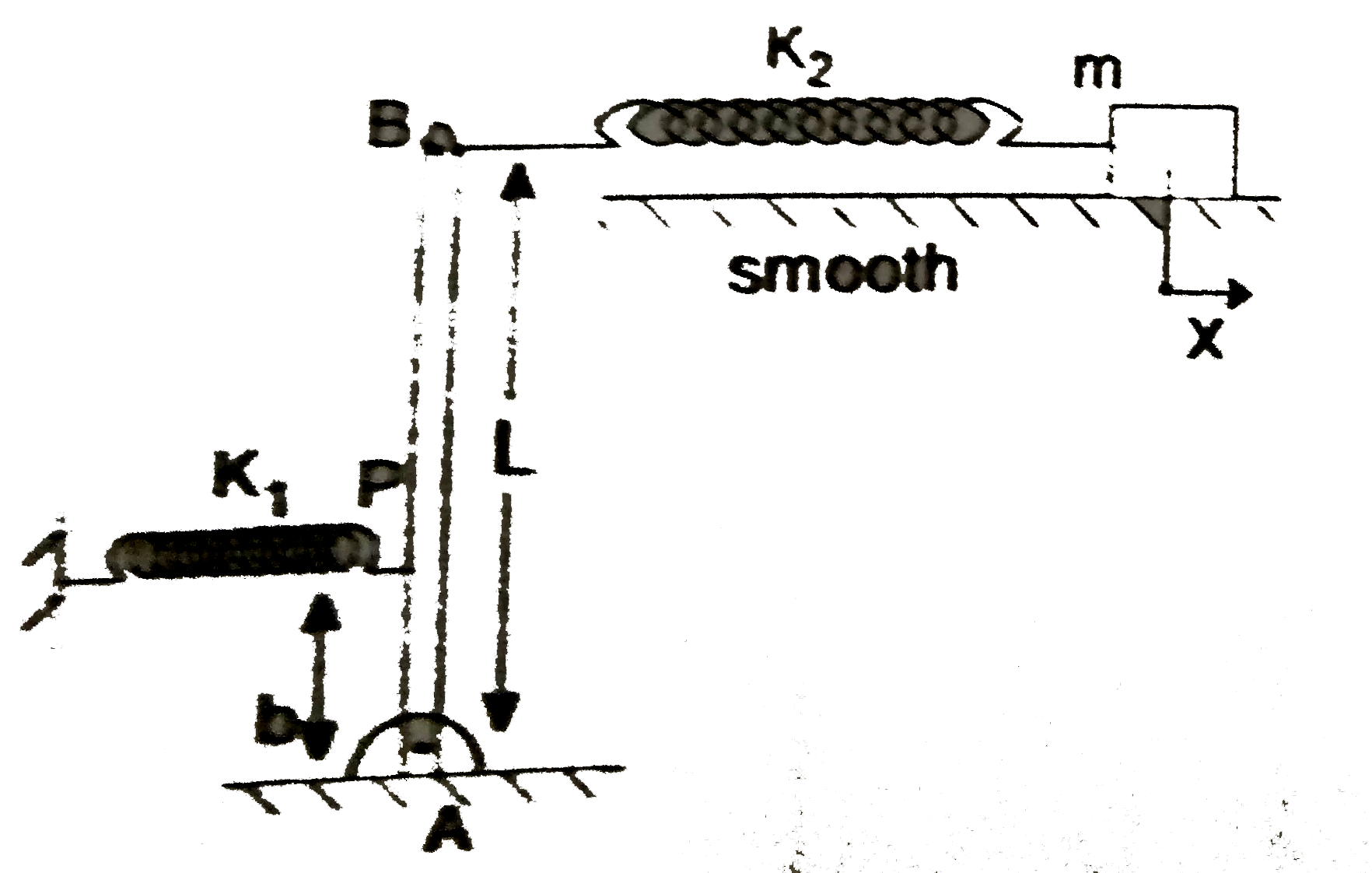
A massless Rod AB is hinged at point A. At point P, it is connected by a spring of stiffness K1 and at point B it is connected to another spring of stiffness K2 connected to mass m as shown in figure the length of Rod AB is l and displaced by a distance x from its mean position as shown in figure then the time period of S.H.M. of mass is
View SolutionForce constants K1andK2 of two springs are in the ratio 5:4. They are stretched by same length. If potential energy stored in one spring is 25 J then potential energy stored in second spring is
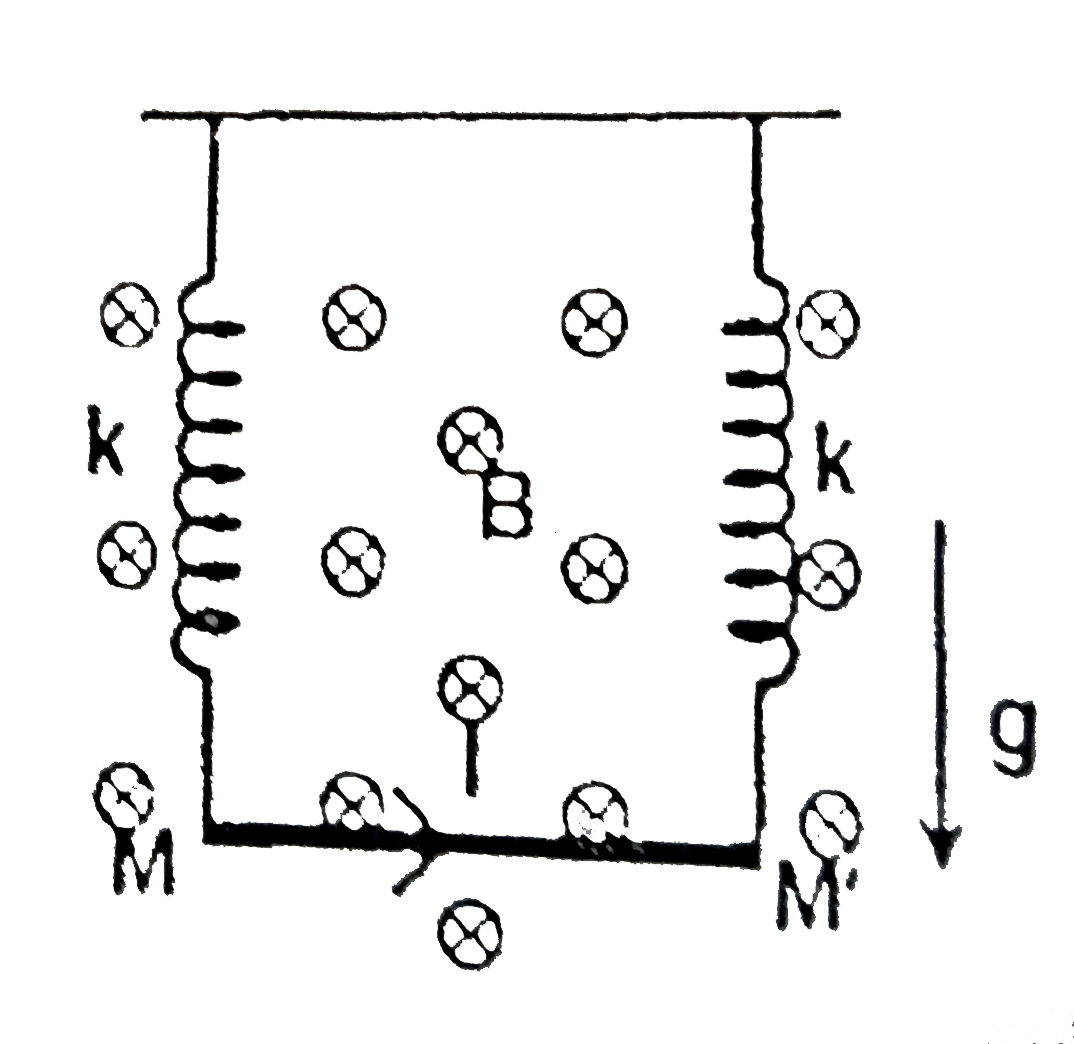
View SolutionConsider the plane of the paper to be vertical plane with direction of 'g' as shown in the figure. A rod (MM') of mass 'M' and carrying a current I. The rod is suspended vertically through two insulated spring of spring constant K at two ends. A uniform magnetic field is applied perpendicular to the plane of the paper such that the potential energy stored in the spring, in equilibrium position is zero. If the rod is slightly displaced in the vertically direction from the position of equilibrium, then the time period of oscillation is
View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
View Solution
