A body of mass m hangs by an inextensible string that passes over a smooth mass less pulley that is fitted with a light spring of stiffness k as shown in figure. If the body is released from rest and the spring is released, calculate the maximum elongation of the spring.
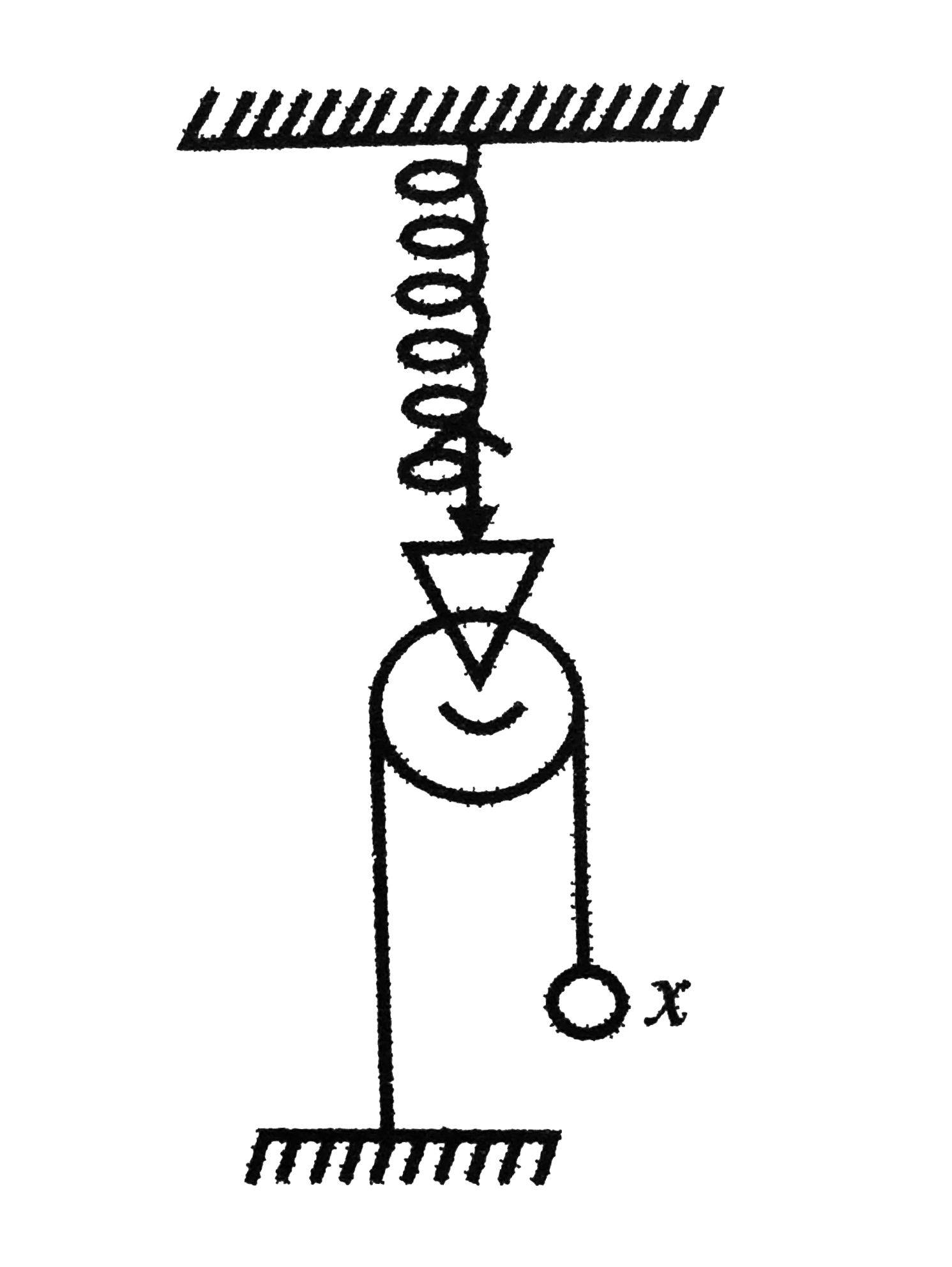
Let the spring be elongated by x. That means the pulley falls through a distance x.
Consequently the string of the pulley is slackened to the same extent x. Therefore, the total distance moved by the body is 2x. Since the spring is elongated by x,
ΔPEspring=12kx2
As the body falls through a distance 2x,
(ΔPE)gr=−mg(2x)
Since the body is initially at rest and comes to rest just at the instant of maximum elongation of the spring, ΔPE=0
Applying the principle of conservation of energy, we get
(ΔPE)+(ΔKE)=0
⇒ΔPESpring+ΔPEgr+ΔKE=0
12kx2−mg(2x)+0=0⇒x=4mgk
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Solved Examples
Explore 15 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
In an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View SolutionTwo block of masses m1 and m2 are in equilibrium. The block m2 hangs from a fixed smooth pulley by an inextensible string that is fitted with a light spring of stiffness k as shown in fig. Neglecting friction and mass of the string, find the acceleration of the bodies just after the string S is cut.

View Solution
Knowledge Check
A disc of mass m is connected with an ideal spring of stiffness k. If it is released from rest, it rolls without sliding on an inclination plane. The maximum elongation of the spring is:
 AmgsinθkB2mgsinθ3kC3mgsinθkD2mgsinθk
AmgsinθkB2mgsinθ3kC3mgsinθkD2mgsinθkA rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .
 A(mg)24kB(mg)22kC(mg)28kD(mg)2k.
A(mg)24kB(mg)22kC(mg)28kD(mg)2k.A block of mass 2 m hangs by an inextensible light string that passes over a smooth pulley. Another mass m hangs from the other end of the string and is connected to a vertical massless spring. The system is stationary. Just after the string is cut, the accelerations of m and 2m, respectively, are -
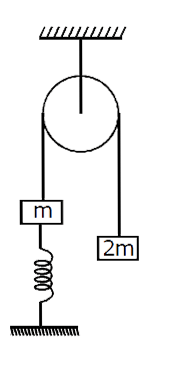 A0,0B0,g↓Cg2⏐⏐ ⏐↓g⏐⏐ ⏐↓D2g↓,g↓
A0,0B0,g↓Cg2⏐⏐ ⏐↓g⏐⏐ ⏐↓D2g↓,g↓
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass m is relesed from rest from a height h onto a smooth sledge of mass M fitted with an ideal spring of stiffness k.

View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of mass 2M is attached to a massless spring with spring-constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1a2 and a3 as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0 Which of the following option(s) is(are) correct? [g is the acceleration due to gravity. Neglect friction]
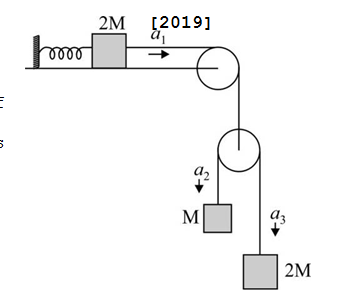
View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 .
.
View Solution

