A thin uniform vertical rod of mass m and length l pivoted at point O is shown in Fig. The combined stiffness of the springs is equal to k. The mass of the springs is negligible. The angular frequency of small oscillation is
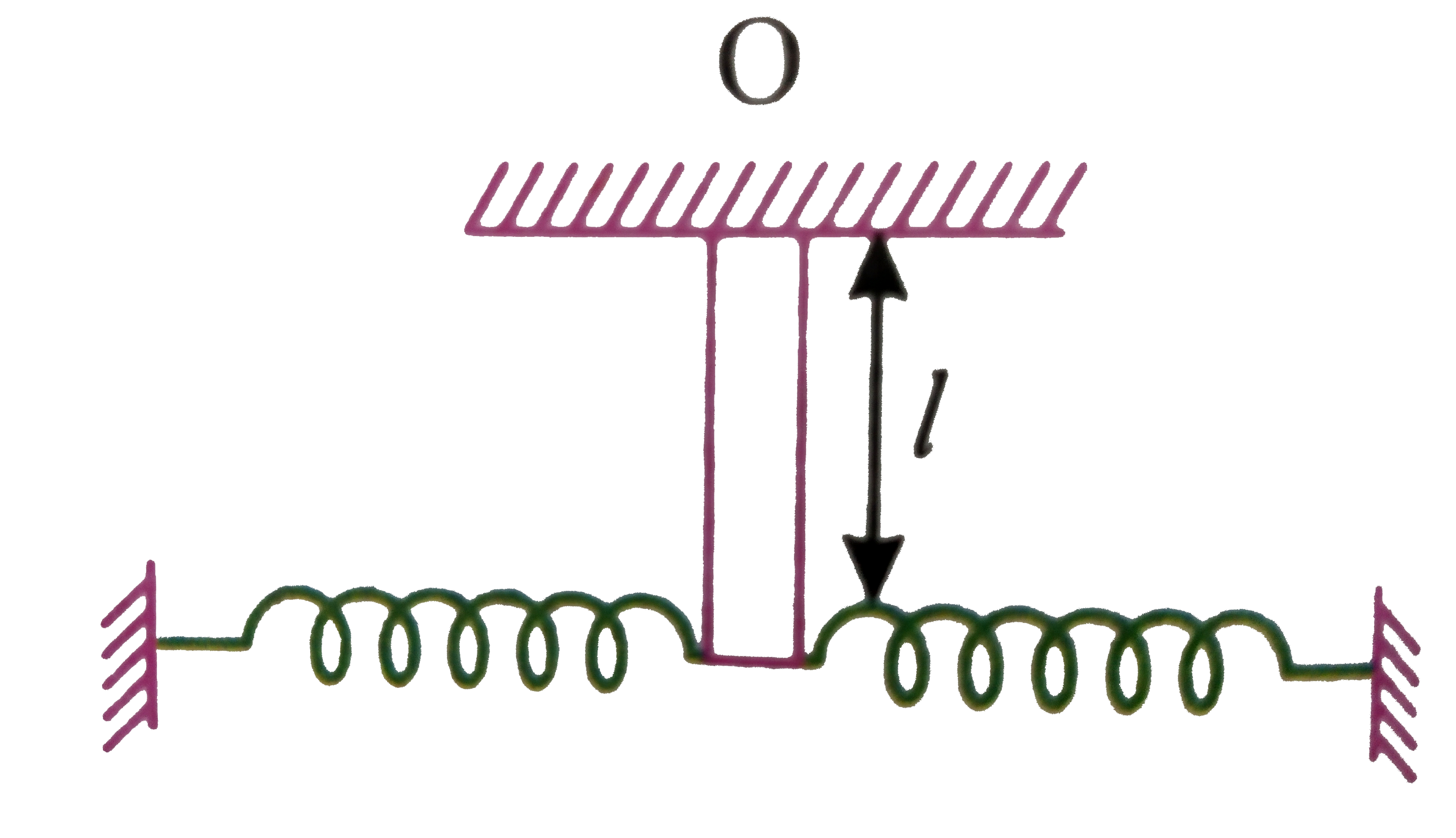
√3k2m+gl
√3k2m+3gl
√3km+3g2l
√3km+2g3l
The correct Answer is:C
Let the diagram in disturbed position is as shown.
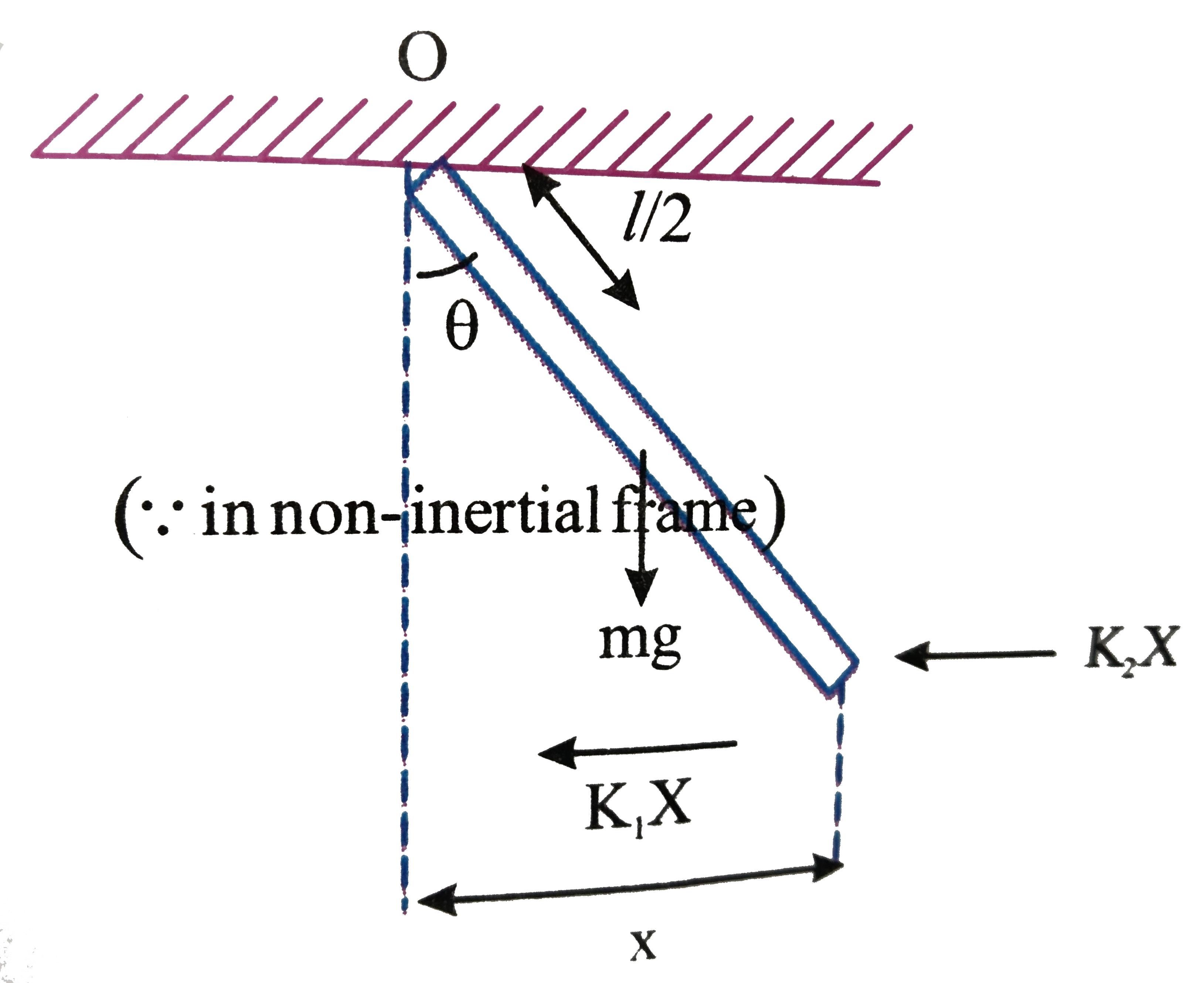
∴ Restoring torque about 'O' is
τrest=mg(l2)sinθ+k1x(lcosθ)+k2x(lcosθ)
=mgl2sinθ+kxlcosθ(∵k1+k2=k)
1(∵θ→small,sinθ→θ,cosθ→1,x=lθ)=[mgl2+kl2]θ,
=I.α=ml23.α⇒α=ω2θ⇒ω=?
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-I
Explore 2 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage
Explore 33 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL-V
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
Find the frequency of small oscillatinos of a thin uniform vertical rod of mass m and length l hinged at the point O (figure). The combined stiffness fo the springs is equal to x. The mass of the springs is negligible.
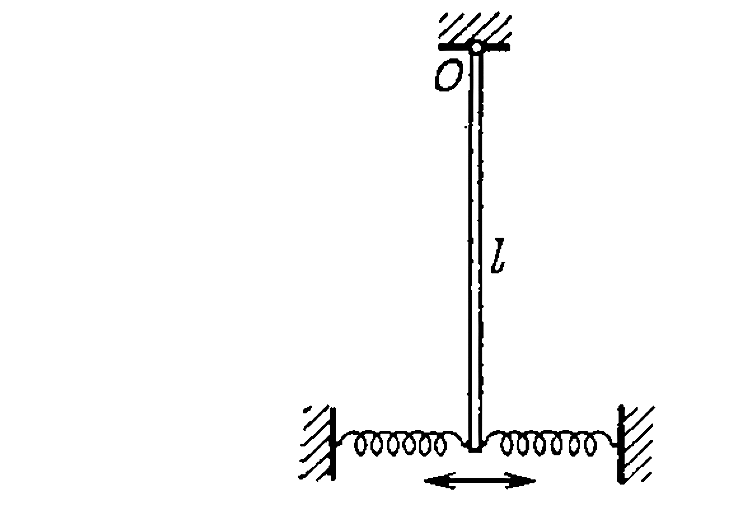
View SolutionIf the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
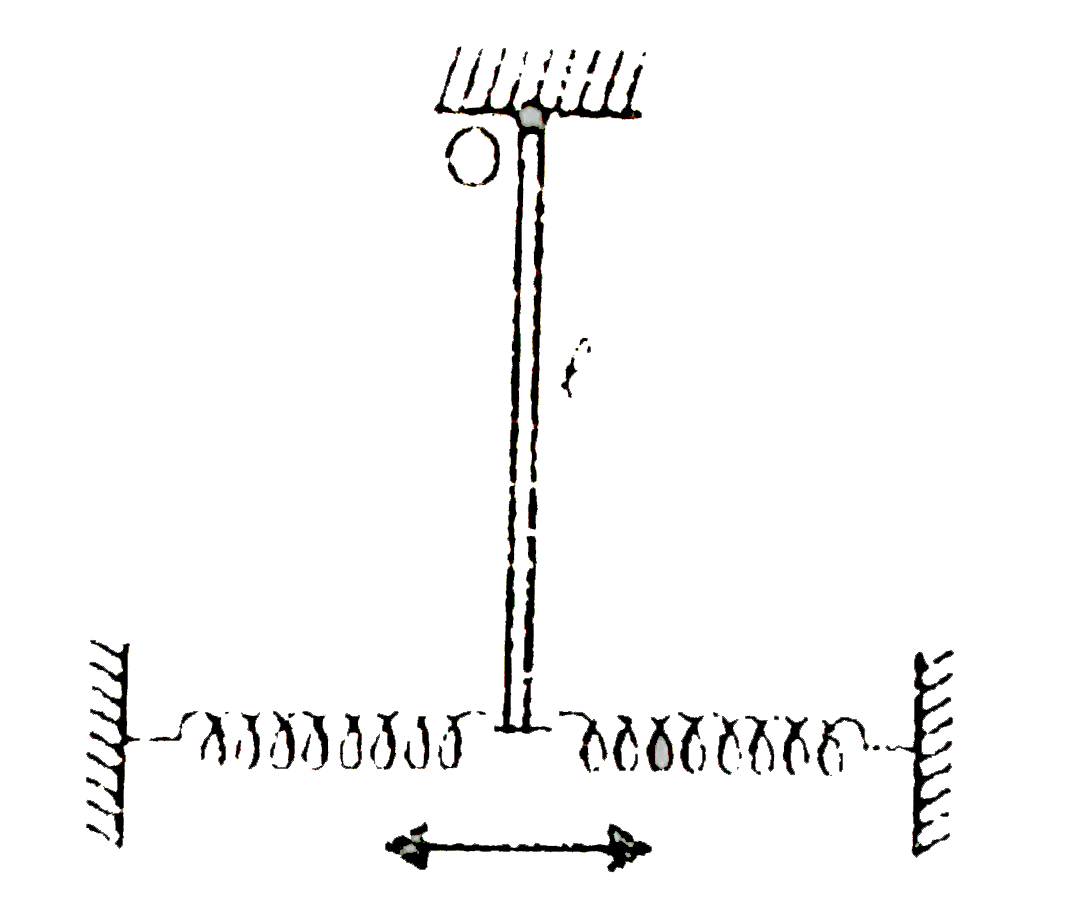
View Solution
Knowledge Check

A thin uniform vertical rod of mass m and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to k. The mass of the spring is negligible. The frequency of small oscillation is .A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3lA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gA body of mass m, is attached to a vertical rod of mass M nad length L, hung from a pivoted supprot. A springs of constant K fixed to a support on the left as shown and is attached to the rod at a distance form the pivot. The frequency of the oscillation is:
 A12π√K(M+2m)B12π ⎷K(M3+2m)C2π ⎷K(M3+2m)D2π√M+2mK
A12π√K(M+2m)B12π ⎷K(M3+2m)C2π ⎷K(M3+2m)D2π√M+2mK
If the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
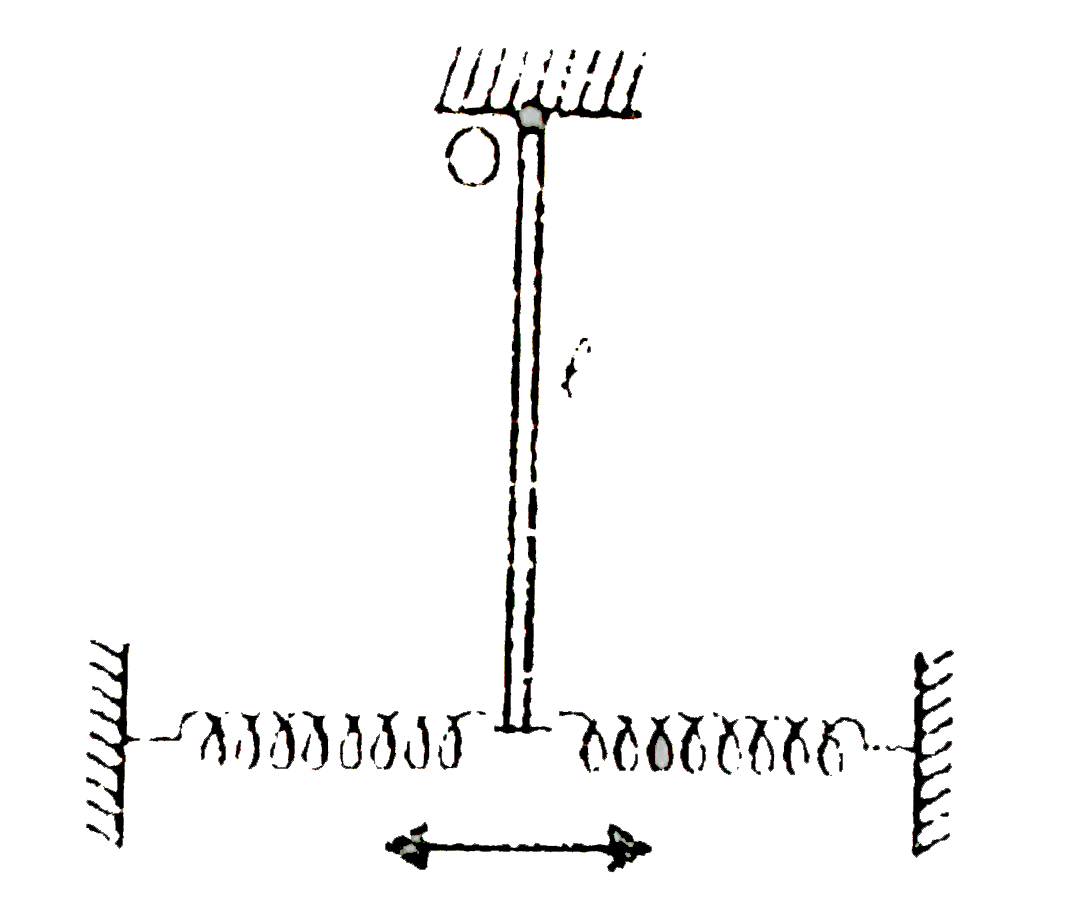
View SolutionFind the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.

View Solution
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View SolutionA system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?

View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.

View Solution